What is the Common Ratio?
A common ratio (r) is a non-zero quotient obtained by dividing each term in a series by the one before it. The formula is:
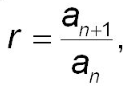
.
You could use any two consecutive terms in the series to work the formula. For example, the 2nd and 3rd, 4th and 5th, or 35th and 36th.
Common Ratio Examples
In a geometric sequence, consecutive terms have a common ratio. For example:
- The series 1, 2, 4, 8, 16, 32, … has an r of 3, because 2/1 = 2, 4/2 = 2, and so on.
- The series 1200, 600, 300, 150, … has an r of ½ because each term is one half of the term before it: 600/1200 = ½, 300/600 = ½…
Watch this one minute video for an example of how to find the common ratio:
Convergence and Divergence
A geometric series diverges when the absolute value of r is greater to or equal to 1 (|r| ≥ 1); the series converges when r < 1.
What is the Common Difference
In an arithmetic sequence, the difference (an addition or subtraction) between any two consecutive terms is a constant. This constant is called a common difference. To find the common difference, subtract a term from the one before it. Watch this one minute video for a quick example of how to find the common difference:
References
University of Toronto Department of Mathematics. Sequences and Series. Retrieved July 10, 2020 from: https://www.math.toronto.edu/preparing-for-calculus/9_sequences/sequences.html