The title might sound daunting, but properties of limits (also called limit laws) are just shortcuts to finding limits of functions.
How To Use Properties of Limits
To find a limit using the properties of limits rule:
- Figure out what kind of function you are dealing with in the list of “Function Types” below (for example, an exponential function or a logarithmic function),
- Click on the function name to skip to the correct rule,
- Substitute your specific function into the rule.
Function Types
Click a function name in the left column to skip to that rule.
| Rule Name | Notation | Example |
| 1. Constant function | f(x) = C | y = 5 |
| 2. Constant multiplied by another function | k * f(x) | 5 * 10x2 |
| 3. Sum of functions | f(x) + g(x) + … | 10x2 + 5x |
| 4. Product of two or more functions | f(x) * g(x) * … | 10x2 * 5x |
| 5.Quotient Law | f(x) / g(x) | 5x / 10x2 |
| 6. Power functions | f(x) = axp | 10x2 |
| 7. Exponential functions | f(x) = bx | 10x |
| 8. Logarithmic functions | f(x) = logbx | log10x |
1. Constant Function
![]() The limit of a constant function C is equal to the constant.
The limit of a constant function C is equal to the constant.
Example: if the function is y = 5, then the limit is 5.
2. Constant Multiplied by a Function (Constant Multiple Rule)
![]() The limit of a constant (k) multiplied by a function equals the constant multiplied by the limit of the function.
The limit of a constant (k) multiplied by a function equals the constant multiplied by the limit of the function.
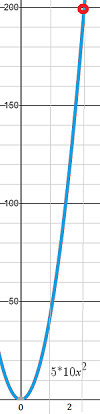
- The limit of f(x) = 5 is 5 (from rule 1 above).
- The limit of 10x2 at x = 2 can be found with direct substitution (where you just plug in the x-value): 10((22) = 40
- Multiply your answers from (1) and (2) together: 5 * 40 = 200
Tip: Plot a graph (using a graphing calculator) to check your answers.
3. Sum of Functions
![]()
The limit of a sum equals the sum of the limits. In other words, figure out the limit for each piece, then add them together.
For step by step examples, see: Sum rule for limits.
4. Product of Two or More Functions
![]()
The limit of a product (multiplication) is equal to the product of the limits. In other words, find the limits of the individual parts and then multiply those together.
Example: Find the limit as x→2 for x2 · 5 · 10x
- The limit of x2 as x→2 (using direct substitution) is x2 = 22 = 4
- The limit of the constant 5 (rule 1 above) is 5
- Limit of 10x (using direct substitution again) = 10(2) = 20
- Multiply (1), (2) and (3) together: 4 · 5 · 20 = 400
Extended Product Rule
![]()
Any “extended” formulas in properties of limits are just extensions of other formulas. This one is just an extension of the product rule above: you can just keep on multiplying as many parts as you need (e.g. a * b * c * d * …).
5. Quotient of Two or More Functions
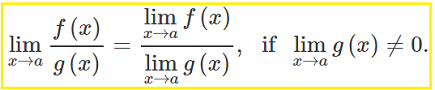
The limit of a quotient is equal to the quotient of the limits. In other words:
- Find the limit for the numerator,
- Find the limit for the denominator,
- Divide the two (assuming that the denominator isn’t zero!).
6. Power Functions
![]()
The rule for power functions states: The limit of the power of a function is the power of the limit of the function, where p is any real number.
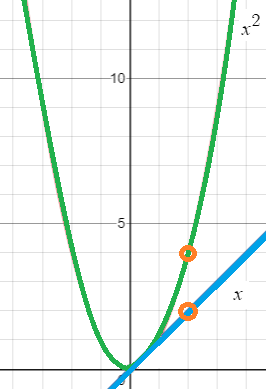 Example: Find the limit of the function f(x) = x2 as x→2.
Example: Find the limit of the function f(x) = x2 as x→2.
- Remove the power: f(x) = x
- Find the limit of step 1 at the given x-value (x→2): the limit of f(x) = 2 at x = 2 is 2. You can use direct substitution or a graph like the one on the left.
- Put the power back in: 22 = 4
A particular case involving a radical:
![]()
Also, if f(x) = xn, then:
![]()
This particular part of the properties of limits “rule” for power functions is really just a shortcut: The limit of x power is a power when x approaches a.
7. Exponential Functions
![]()
8. Logarithmic Functions
![]()
Properties of Limits: References
Gunnels, P. (undated). Limit Laws. Retrieved May 29, 2019 from: http://people.math.umass.edu/~gunnells/teaching/Sample_Lecture_Notes.pdf