Shape Parameter: Definition and Examples

Statistics Definitions > Shape Parameter

What is a Shape Parameter?

A shape parameter, as the name suggests, affects the general shape of a distribution; they are a family of distributions with different shapes. The parameters are usually known from prior statistical data or they are sometimes estimated from current data.

For example, the Beta distribution has a shape parameter. Changing this parameter changes the overall shape of the graph.

In contrast, several other distributions do not have these parameters. They include the exponential distribution. Even though the exponential distribution can be squeezed, stretched, or shifted, the overall shape remains the same.

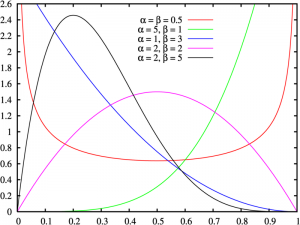
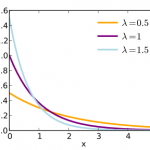
The most important thing to grasp about the shape parameter is that it doesn’t change where the graph lies on the horizontal axis of a Cartesian plane (that’s the job of the location parameter). Nor does it shrink or squeeze the graph (the job of the scale parameter). It just defines the general shape of the graph for certain distributions.

In some distributions (like the Weibull distribution), the parameter can help define skewness. For example:

• Larger parameters tend to result in a left-skewed distribution.
• Smaller parameters tend to result in a right-skewed distribution.

This is not a universal rule though, just a general guideline.

Other Parameters that Affect Shapes of Distributions

Some of the other parameters used to define distributions:

• The Location parameter tells you where the distribution is centered on the horizontal axis.
• The Scale parameter gives you an idea of the scale on the horizontal axis. For example, the scale parameter on a standard normal distribution is equal to one standard deviation (σ). It usually stretches or squeezes a graph.

References

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.