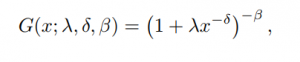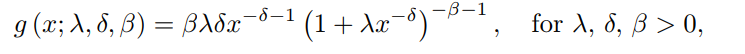Probability Distributions > Dagum distribution
The Dagum distribution (also called the Inverse Burr distribution; Dagum called it the generalized logistic-Burr distribution) was proposed by Camilo Dagum in the 1970s to model income and wealth. Dagum developed the models as an alternative to the Pareto Distribution and lognormal distribution, which he felt didn’t result in accurate models when applied to spread of income. More specifically, Dagum wasn’t satisfied with how the Pareto and lognormal handles heavy-tailed data. Specifically, he felt a better model could be developed for the heavy tails often found in empirical income and wealth distributions, while allowing for an interior mode. The Pareto handles heavy tails well, but the lognormal does not. And while the lognormal allows an interior mode (or a mode at zero), the Pareto doesn’t. Dagum’s distribution allows for an interior mode and it handles heavy tails (Kleiber, 2007). Despite its relative unpopularity, the Dagum distribution often performs better than other two/three parameter income/wealth distribution models when applied to empirical data.
Dagum Distribution CDF and PDF
The CDF of the Type I (three parameter) Dagum distribution is: 
The PDF is: 
Where:
- λ = a scale parameter,
- δ and Β = shape parameters.
When Β = 1, the distribution is called the log-logistic distribution.
Types
The three parameter Dagum Type I distribution evolved from Dagum’s experimentation with a shifted log-logistic distribution (Chotikapanich, 2008). Two four-parameter (Type II) generalizations were also developed.
Real World Applications of the Dagum Distribution
Since its development in 1974, researchers have used the Dagum distribution to analyze various types of data related to income inequality and poverty levels across different regions. For example, many researchers have studied how changes in GDP per capita affect poverty levels using this distribution model. Other researchers have used it to study regional disparities in wages within countries or even global trends in wealth distribution between nations. Additionally, many economists use this model when making predictions about future economic growth or planning policy related to taxation or welfare spending.
References
PDF Image: Rafael Marcondes, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons
Atkinson, A. (2014). Handbook of Income Distribution, Volume 2. Elsevier.
Chotikapanich, D. (Ed.) (2008). Modeling Income Distributions and Lorenz Curves. Springer Science & Business Media.
Dagum, C., A New Model of Personal Income Distribution: Specification and Estimation, Economie Applique’e, 30, 413 – 437, (1977).
Kleiber, C. & Kotz, S. (2003). Statistical Size Distributions in Economics and Actuarial Sciences. John Wiley & Sons.
Kleiber, C. (2007). A Guide to the Dagum Distributions. Retrieved May 26, 2020 from: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=BEE8C9083715B6042596B0DC170BFDA1?doi=10.1.1.610.8346&rep=rep1&type=pdf