What is a Non Parametric Test?
A non parametric test (sometimes called a distribution free test) does not assume anything about the underlying distribution (for example, that the data comes from a normal distribution). That’s compared to parametric test, which makes assumptions about a population’s parameters (for example, the mean or standard deviation); When the word “non parametric” is used in stats, it doesn’t quite mean that you know nothing about the population. It usually means that you know the population data does not have a normal distribution.
For example, one assumption for the one way ANOVA is that the data comes from a normal distribution. If your data isn’t normally distributed, you can’t run an ANOVA, but you can run the nonparametric alternative—the Kruskal-Wallis test.
If at all possible, you should us parametric tests, as they tend to be more accurate. Parametric tests have greater statistical power, which means they are likely to find a true significant effect. Use nonparametric tests only if you have to (i.e. you know that assumptions like normality are being violated). Nonparametric tests can perform well with non-normal continuous data if you have a sufficiently large sample size (generally 15-20 items in each group).
When to use it
Non parametric tests are used when your data isn’t normal. Therefore the key is to figure out if you have normally distributed data. For example, you could look at the distribution of your data. If your data is approximately normal, then you can use parametric statistical tests.
Q. If you don’t have a graph, how do you figure out if your data is normally distributed?
A. Check the skewness and Kurtosis of the distribution using software like Excel (See: Skewness in Excel 2013 and Kurtosis in Excel 2013).
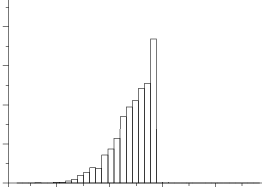
A normal distribution has no skew. Basically, it’s a centered and symmetrical in shape. Kurtosis refers to how much of the data is in the tails and the center. The skewness and kurtosis for a normal distribution is about 1.
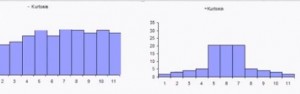
If your distribution is not normal (in other words, the skewness and kurtosis deviate a lot from 1.0), you should use a non parametric test like chi-square test. Otherwise you run the risk that your results will be meaningless.
Data Types
Does your data allow for a parametric test, or do you have to use a non parametric test like chi-square? The rule of thumb is:
- For nominal scales or ordinal scales, use non parametric statistics.
- For interval scales or ratio scales use parametric statistics.
- One or more assumptions of a parametric test have been violated.
- Your sample size is too small to run a parametric test.
- Your data has outliers that cannot be removed.
- You want to test for the median rather than the mean (you might want to do this if you have a very skewed distribution).
Types of Nonparametric Tests
When the word “parametric” is used in stats, it usually means tests like ANOVA or a t test. Those tests both assume that the population data has a normal distribution. Non parametric do not assume that the data is normally distributed. The only non parametric test you are likely to come across in elementary stats is the chi-square test. However, there are several others. For example: the Kruskal Willis test is the non parametric alternative to the One way ANOVA and the Mann Whitney is the non parametric alternative to the two sample t test.
The main nonparametric tests are:
- 1-sample sign test. Use this test to estimate the median of a population and compare it to a reference value or target value.
- 1-sample Wilcoxon signed rank test. With this test, you also estimate the population median and compare it to a reference/target value. However, the test assumes your data comes from a symmetric distribution (like the Cauchy distribution or uniform distribution).
- Friedman test. This test is used to test for differences between groups with ordinal dependent variables. It can also be used for continuous data if the one-way ANOVA with repeated measures is inappropriate (i.e. some assumption has been violated).
- Goodman Kruska’s Gamma: a test of association for ranked variables.
- Kruskal-Wallis test. Use this test instead of a one-way ANOVA to find out if two or more medians are different. Ranks of the data points are used for the calculations, rather than the data points themselves.
- The Mann-Kendall Trend Test looks for trends in time-series data.
- Mann-Whitney test. Use this test to compare differences between two independent groups when dependent variables are either ordinal or continuous.
- Mood’s Median test. Use this test instead of the sign test when you have two independent samples.
- Spearman Rank Correlation.Use when you want to find a correlation between two sets of data.
The following table lists the nonparametric tests and their parametric alternatives.
| Nonparametric test | Parametric Alternative |
|---|---|
| 1-sample sign test | One-sample Z-test, One sample t-test |
| 1-sample Wilcoxon Signed Rank test | One sample Z-test, One sample t-test |
| Friedman test | Two-way ANOVA |
| Kruskal-Wallis test | One-way ANOVA |
| Mann-Whitney test | Independent samples t-test |
| Mood’s Median test | One-way ANOVA |
| Spearman Rank Correlation | Correlation Coefficient |
Advantages and Disadvantages
Compared to parametric tests, nonparametric tests have several advantages, including:
- More statistical power when assumptions for the parametric tests have been violated. When assumptions haven’t been violated, they can be almost as powerful.
- Fewer assumptions (i.e. the assumption of normality doesn’t apply).
- Small sample sizes are acceptable.
- They can be used for all data types, including nominal variables, interval variables, or data that has outliers or that has been measured imprecisely.
However, they do have their disadvantages. The most notable ones are:
- Less powerful than parametric tests if assumptions haven’t been violated.
- More labor-intensive to calculate by hand (for computer calculations, this isn’t an issue).
- Critical value tables for many tests aren’t included in many computer software packages. This is compared to tables for parametric tests (like the z-table or t-table) which usually are included.
References
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
Comments? Need to post a correction? Please Contact Us.