Outliers: Finding Them in Data, Formula, Examples. Easy Steps and Video

Outliers are stragglers — extremely high or extremely low values — in a data set that can throw off your stats. For example, if you were measuring children’s nose length, your average value might be thrown off if Pinocchio was in the class.

Contents (Click to skip to the section):

1. What is an Outlier?
2. How to Find Outliers with the Interquartile Range.
3. How to Find Outliers with the Tukey Method and more advanced methods.

Watch the video for the definition and how to find outliers with the IQR and Tukey’s method:

What is an outlier?

An outlier is a piece of data that is an abnormal distance from other points. In other words, it’s data that lies outside the other values in the set. If you had Pinocchio in a class of children, the length of his nose compared to the other children would be an outlier.
In this set of random numbers, 1 and 201 are outliers:
1, 99, 100, 101, 103, 109, 110, 201
“1” is an extremely low value and “201” is an extremely high value.

Outliers aren’t always that obvious. Let’s say you received the following paychecks last month:
$225, $250, $25, $235.
Your average paycheck is $135. But that small paycheck ($25) might be because you went on vacation, so a weekly paycheck average of $135 isn’t a true reflection of how much you earned. Your average is actually closer to $237 if you take the outlier ($25) out of the set.

Of course, trying to find outliers isn’t always that simple. Your data set may look like this:
61, 10, 32, 19, 22, 29, 36, 14, 49, 3.
You could take a guess that 3 might be an outlier and perhaps 61. But you’d be wrong: 61 is the only outlier in this data set.
A box and whiskers chart (boxplot) often shows outliers:

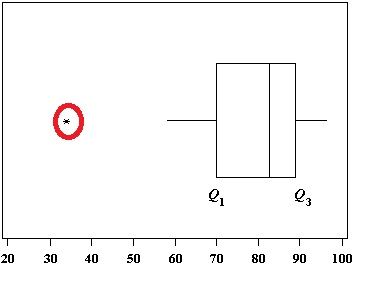
However, you may not have access to a box and whiskers chart. And even if you do, some boxplots may not show outliers. For example, this chart has whiskers that reach out to include outliers: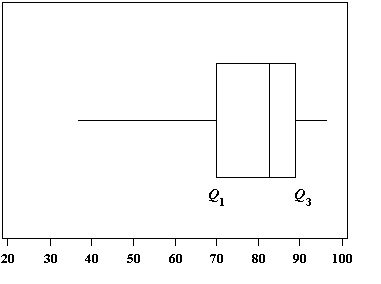

Therefore, don’t rely on finding outliers from a box and whiskers chart. That said, box and whiskers charts can be a useful tool to display them after you have calculated what your outliers actually are. The most effective way to find all of your outliers is by using the interquartile range (IQR). The IQR contains the middle bulk of your data, so outliers can be easily found once you know the IQR.
Back to Top

How to Find Outliers Using the Interquartile Range(IQR)

Need help with a homework question? Check out our tutoring page!

An outlier is defined as being any point of data that lies over 1.5 IQRs below the first quartile (Q₁) or above the third quartile (Q₃)in a data set.
High = (Q₃) + 1.5 IQR
Low = (Q₁) – 1.5 IQR

Example Question: Find the outliers for the following data set: 3, 10, 14, 22, 19, 29, 70, 49, 36, 32.

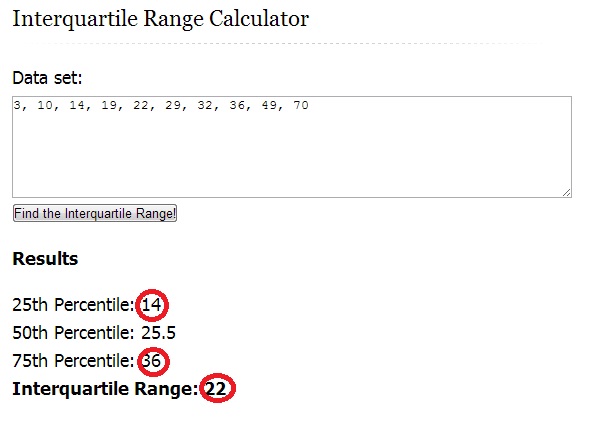
Step 1: Find the IQR, Q₁(25th percentile) and Q₃(75th percentile). Use our online interquartile range calculator to find the IQR or if you want to calculate it by hand, follow the steps in this article: Interquartile Range in Statistics: How to find it.
IQR = 22
Q₁ = 14
Q₃ = 36

Step 2: Multiply the IQR you found in Step 1 by 1.5:
IQR * 1.5 = 22 * 1.5 = 33.

Step 3: Add the amount you found in Step 2 to Q₃ from Step 1:
33 + 36 = 69.

This is your upper limit. Set this number aside for a moment.

Step 3: Subtract the amount you found in Step 2 from Q₁ from Step 1:
14 – 33 = -19.
This is your lower limit. Set this number aside for a moment.

Step 5: Put the numbers from your data set in order:
3, 10, 14, 19, 22, 29, 32, 36, 49, 70

Step 6: Insert your low and high values into your data set, in order:
-19, 3, 10, 14, 19, 22, 29, 32, 36, 49, 69, 70

Step 6: Highlight any number below or above the numbers you inserted in Step 6:
-19, 3, 10, 14, 19, 22, 29, 32, 36, 49, 69, 70

That’s it!
Back to Top

How to Find Outliers with the The Tukey Method

The Tukey method for finding outliers uses the interquartile range to filter out very large or very small numbers. It’s practically the same as the procedure above, but you might see the formulas written slightly differently and the terminology is a little different as well. For example, the Tukey method uses the concept of “fences”.

The formulas are:
Low outliers = Q1 – 1.5(Q3 – Q1) = Q1 – 1.5(IQR)
High outliers = Q3 + 1.5(Q3 – Q1) = Q3 + 1.5(IQR)
Where:
Q1 = first quartile
Q3 = third quartile
IQR = Interquartile range

These equations give you two values, or “fences“. You can think of them as a fence that cordons off the outliers from all of the values that are contained in the bulk of the data.

Sample question: Use Tukey’s method to find outliers for the following set of data: 1,2,5,6,7,9,12,15,18,19,38.
Step 1: Find the Interquartile range:

1. Find the median: 1,2,5,6,7,9,12,15,18,19,38.
2. Place parentheses around the numbers above and below the median — it makes Q1 and Q3 easier to find.
   (1,2,5,6,7),9,(12,15,18,19,38)
3. Find Q1 and Q3. Q1 can be thought of as a median in the lower half of the data. Q3 can be thought of as a median for the upper half of data.
   (1,2,5,6,7), 9, ( 12,15,18,19,38). Q1=5 and Q3=18.
4. Subtract Q1 from Q3. 18-5=13.

Step 2: Calculate 1.5 * IQR:
1.5 * IQR = 1.5 * 13 = 19.5

Step 3: Subtract from Q1 to get your lower fence:
5 – 19.5 = -14.5

Step 4: Add to Q3 to get your upper fence:
18 + 19.5 = 37.5.

Step 5:Add your fences to your data to identify outliers:
(-14.5) 1,2,5,6,7,9,12,15,18,19,(37.5),38.
Anything outside of the fences is an outlier. For this data set, 38 is the only outlier.

That’s how to find outliers with the Tukey method!

Back to Top

How to Find Outliers with Advanced Methods

1. Generalized ESD
2. Grubbs’ test.
3. Dixon’s Q Test.
4. Modified Thompson Tau Test
5. Peirce’s Criterion

Next: Modify Extreme Values with Winsorizations

References

Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wang.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Tukey, J. Exploratory Data Analysis, Addison-Wesley, 1977, pp. 43-44.

Check out our YouTube channel for more stats tips and help!