Nonparametric data and tests >
The gamma coefficient (also called the gamma statistic, or Goodman and Kruskal’s gamma) tells us how closely two pairs of data points “match”. Gamma tests for an association between points and also tells us the strength of association. The goal of the test is to be able to predict where new values will rank. For example, if score A scores “LOW” for question 1 and “HiGH” for question 2, will score B also result in a LOW/High response?
Gamma can be calculated for ordinal (ordered) variables that are continuous variables (like height or weight) or discrete variables (like “hot” “hotter” and “hottest”). While there are other coefficients that can calculate relationships for these types of variables, like Somer’s D or Kendall’s Tau, Goodman and Kruskal’s gamma is generally preferred for when you have many tied ranks. It is also particularly useful when your data has outliers, as they don’t affect the results much. For some fields of study it may be the preferred method for all ordinal data arranged in a bivariate table. If you have two dichotomous variables (e.g. responses that are yes/no), use Yule’s Q instead.
Range of the Gamma Coefficient
The gamma coefficient ranges between -1 and 1.
- 1 = perfect positive correlation: if one value goes up, so does the other.
- -1 = perfect inverse correlation: as one value goes up, the other goes down.
- 0 = there is no association between the variables
The closer you get to a 1 (or -1), the stronger the relationship. You can deduce the significance of your result by running a significance test for gamma (see below). But how strong these relationships need to be depend upon which field of study you’re working in. For example, a .75 might be “strong enough” in one field while another might require over .8.
You can interpret gamma as the proportion of ranked pairs in agreement. For example, if gamma = +1, it means that every single pair in your experiment is in agreement, or that every rater has agreed upon which order the items should be ranked.
Gamma treats the variables symmetrically; you don’t have to hypothesize which might be dependent and which might be independent variables.
Calculating the Gamma Coefficient
Goodman and Kruskal’s gamma uses the following formula:
![]()
Where:
- Nc is the total number of pairs that rank the same (concordant pairs)
- Nd is the number of pairs that don’t rank the same (discordant pairs).
Example 1 (Simple 2×2)
Suppose you are analyzing data on hours spent studying versus test scores. You might hypothesize that more studying will lead to better grades, and you collect data that might show that. To make it simple, you’ll define minimal studying as less than one hour a week, and extensive studying as anything more than that. You’ll also define good grades as A and A+, with bad grades being anything below. You can tabulate your hypothetical data like this:
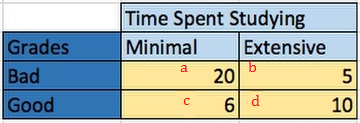
Cells a and d (minimal time/bad scores and extensive time/ good scores) are those that support your hypothesis (i.e. they are concordant). Cells b and c go the other direction; If significant, they go against your hypothesis and are non-supporting (discordant).
To calculate the gamma coefficient:
- Find the number of concordant pairs, Nc Start with the upper left square and multiply by the sum of all agreeing squares below and to the right (in this case, just d). Nc = 10 * 20 = 200,
- Find the number of disconcordant pairs. Nd is calculated the same way; now, start with the upper right square and multiply by the sum of all ‘non-supporting’ squares below and to the right. Do this again for every non-supporting square, working down and left.
Nd = 5 * 6 = 30. - Insert the values from Step 1 into the formula:
The gamma statistic is:
(Nc – Nd) / (Nc + Nd) =
(200 – 30) / (200 + 30), or 0.7391.
Since the gamma coefficient is much closer to 1 (perfect correlation) than to 0 (no association), your data points to a strong correleation and your hypothesis has a good chance of being correct.
Example 2 (Complex)
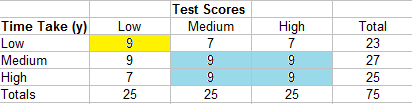
This works with a more complicated table:
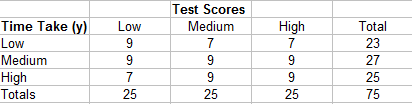
As before, find Ncby multiplying each cell by the sums of the cells and then adding those sums together. Identifying the cells you’ll need in the equation is more easily explained in a step-by-step example.
- Start with the top left cell (9). The cells below and to the right of it are 9,9,9, and 9.

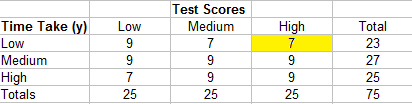
- Move over to the next cell (7). The two cells below and to the right are 9 and 9.

- Move over to the next cell (7). There are no cells to the right of this cell.

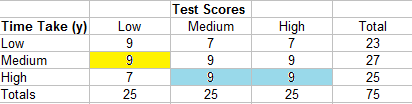
- Move down to the next row. The first cell (9) has two cells to the right and bottom (9,9).

- Continue down the table until all the cells have been accounted for.
The summary of cells for this example is:
- 9 (9 + 9 + 9 + 9) = 324
- 7 (9 + 9) = 126
- 7 (0) = 0
- 9 (9 + 9) = 162
- 9 (9) = 81
- 9 (0) = 0
- 7 (0) = 0
- 9 (0) = 0
- 9 (0) = 0
Adding those all together, we have:
Nc = 324 + 162 + 81 + 126 = 693
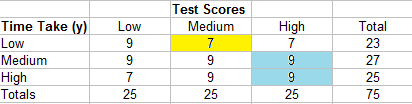
Find the Nd in the same way, only this time start in the top right and count all of the cells to the left and bottom.
- 7 (9 + 9 + 7 + 9) = 238
- 7 (9 + 7) = 112
- 9 (0) = 0
- 9 (9 + 7) = 144
- 9 (7) = 63
- 9 (0) = 0
- 9 (0) = 0
- 9 (0) = 0
- 7 (0) = 0
Adding those all together, we have:
Nd = 238 + 112 + 144 + 63 = 557
Which means Gamma is:
(693 – 557) / (693 + 557) = 0.12
There is a practically no significance (0.12 is close to zero)
Testing for Significance
The gamma test for significance works like most other hypothesis tests: find a test statistic and compare it to a table value. I skim over the steps here, so if you’ve never performed a hypothesis test before you may want to read this article: What is Hypothesis Testing?
The formula for the test statistic is:
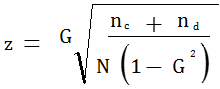
Inserting the values from example 2 above, we have:
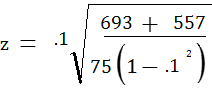
= .4103
The z-table value (for a 5% alpha level) is 1.96. (Not sure how to read a z-table? See: How to read a z-table).
Z = .41 < Zcrit= ± 1.96
As .41 is less than the z critical value, we cannot reject the null hypothesis that there is a difference in the populations.
Yule’s Q
Yule’s Q is just the 2×2 version of the gamma coefficient.The formula is exactly the same, but you are only using cells a,b,c,d. As you’ll never be calculating more concordant / discordant pairs than the ones found in those cells, you’ll see the formula written more commonly as:
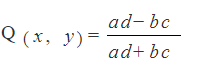
To calculate Yule’s Q, follow the steps in the simple 2×2 example above.
Yule’s Q & Odds Ratio
The odds ratio formula is (a*d) / (b*c). A simple formula, using Yule’s Q, converts the odds ratio to a -1 to +1 scale:
(OR – 1) / (OR + 1)
Interpreting Yule’s Q
Yule’s Q is always a number between -1 and 1.
Q is 0: no association between the variables.
Q = 0 to ± 0.29: a negligible or very small association.
Q = -0.30 to -0.49 or 0.30 to 0.49: a moderate association between the variables.
Q = 0.50 and 0.69 or -0.50 and -0.69: a substantial association between the variables.
Q > 0.70, or < -0.70: a very strong association.
If Q is 1 or -1, there is a perfect association between the events.
A positive Q points to a positive correlation — if x is positive, y is likely to be positive also. A negative Q points to a negative correlation —if x is positive, y is likely to be negative.
References
Bernard, H. Social Research Methods: Qualitative and Quantitative Approaches. Retrieved November 10, 2017 from: https://books.google.com/books?id=VDPftmVO5lYC
Adeyemi, O. (2011) Measures of Association for Research in Educational Planning and Administration. Research Journal of Mathematics and Statistics 3(3): 82-90. Retrieved November 10, 2017 from: http://maxwellsci.com/print/rjms/v3-82-90.pdf
Analysis of Categorical Data
Tests of Association for Ordinal Data. Retrieved February 3, 2020 from: https://www.angelo.edu/faculty/ljones/gov3301/block14/objective4.htm