Derivative of ln (Natural Log), ln(kx), ln(x^2)

Contents:

• Definition of ln
• Derivative of ln

What is a Natural Logarithm?

A natural logarithm (ln) is the inverse function of e^x; It is a logarithm with base e (the base is always a positive number). In other words, y = ln x is the same thing as:

e^y = x
This fact comes into play when we’re finding the derivative of the natural log.

It’s called the natural logarithm because of the “e” (Euler’s number). Mercator (1668) first used the term “natural” (in the Latin form log naturalis) for any logarithm to base e (as cited in O’Connore & Robertson, 2001).

What is the Derivative of ln?</der”>

The derivative of ln(x) or ln(kx) is 1/x. In notation, that’s:

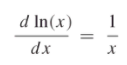
The natural log function, and its derivative, is defined on the domain x > 0.

The derivative of ln(k), where k is any constant, is zero.

The second derivative of ln(x) is -1/x². This can be derived with the power rule, because 1/x can be rewritten as x^-1, allowing you to use the rule.

Derivative of ln: Steps

To find the derivative of ln(x), use the fact that y = ln x can be rewritten as

e^y = x.
Step 1: Take the derivative of both sides of e^y = x:

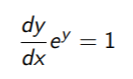
Step 2: Rewrite (using algebra) to get:

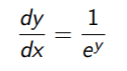
Step 3: Substitute ln(x) for y:

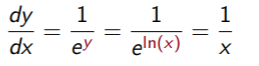
References

Exponential Review. Retrieved November 12, 2021 from: https://mste.illinois.edu/malcz/ExpFit/REVIEW-answers.html
Adler, F. (2013). Modeling the Dynamics of Life: Calculus and Probability for Life Scientists. Cengage Learning.
Daugherty, Z. (2011). Derivatives of Exponential and Logarithm Functions.
O’Connor, J. & Robertson, E. (2001). The Number e. Retrieved August 20, 2020 from: https://mathshistory.st-andrews.ac.uk/HistTopics/e/#:~:text=In%201668%20Nicolaus%20Mercator%20published,for%20logarithms%20to%20base%20e.
Ping, X. (2016). Why natural constant “e” is called “natural”.