What is a Boundary Point?
Generally speaking, a “boundary point” is the edge or border of a set.
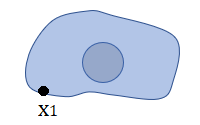
The set of all boundary points is called a boundary [1]. Visually, it’s the line that circumscribes the set. For example, the boundary of a circular set (i.e. one defined by the formula x2 + y2 < 1) is the circumference.
Boundaries aren’t perfect lines; They are collections of point, some of which are inside the set and some are outside. As an example, zoom in on the image above and you’ll see that the boundary is actually a series of tiny printed dots. Some of the dots are inside the set, and some are outside:
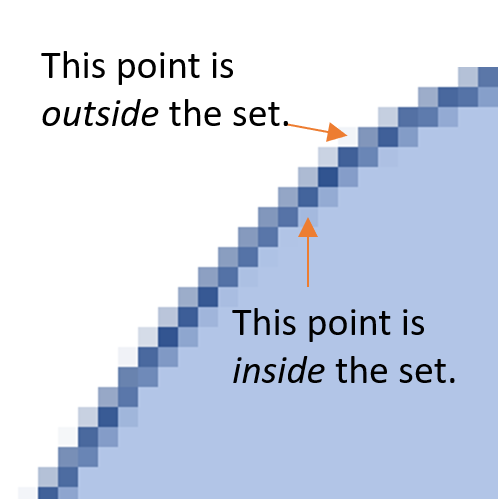
A boundary point then, is neither an interior point (which is definitely in a set) or an exterior point (which is definitely outside the set).
Formal Definition of Boundary Points
Formally speaking, a point x is a boundary point for a region R if every neighborhood (a set of points that are in the same general area) of x intersects both R and the complement of R.
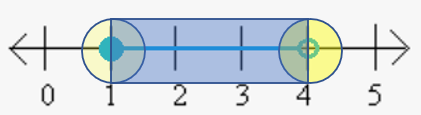
This formal definition may be easier to wrap your head around if you look at an example on the number line.
Let’s say R = [1, 4) has boundary points of 1 and 4. If you draw the set on a number line, it’s clear that the neighborhoods of 1 and 4 intersect the defined set and it’s complement.
Boundary Point vs. Limit Point
A limit point isn’t a “limit ” in the usual calculus sense of the word, but the two terms are related. A limit point is very close to a set, so close in fact in can actually be in the set (and often is).
Limit points and boundary points are similar in that neither have to be in the set. The difference is in their neighborhoods:
- A limit point has a neighborhood containing at least one point belonging to the set.
- A boundary point has a neighborhood with a point belonging to the set and a point not belonging in the set.
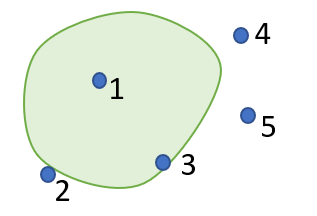
Every boundary point of a set is a limit point [2]. Not every limit point is a boundary point: point 1 is a limit point (it’s also an interior point), but it is not on the boundary.
References
[1] LaValle, S. (2006). Planning Algorithms. Retrieved April 3, 2021 from: http://planning.cs.uiuc.edu/node127.html
[2] Buckmire, R. (2004). Multivariable Calculus. Retrieved April 3, 2021 from: https://sites.oxy.edu/ron/math/224/04/ws/12.pdf