Work: Definition, Calculation by Integration

Calculus Definitions >

Contents (Click to skip to that section):

1. Work (Definition)
2. Work by Integration

1. Definition

Work, in calculus and physics, tells us the amount of energy needed to perform a physical task.  The most common units of measurement are:

• Newton-meters (Nm),
• Joules (J),
• Foot-pound (ft-lb). 

You’ll typically come across two different types of problems . 

1. The force applied is constant. 
2. The force changes over time. 

Formulas

Which formula you use depends on whether or not the force is constant:

1. Work with Constant force

The first formula, work = force * Distance, is used where the force applied is constant.  Solving these types of problems is relatively easy.  All you have to do is multiply force by distance.

Example

Example question: How much work do we need to do to lift a 30 lb box 4 feet off the ground?

Since the force applied is constant, plug the numbers into the first formula:

• w = force x distance
• w = 30 lbs x 4 feet
• w = 120 ft/lbs

To move a 30 lb box 4 feet off the ground requires 120 ft/lbs.

2. Work with Varying Level of Force

The second formula, which involves integration, is used where the force applied changes over time.  In this formula,

• w is work,
• f(x) is force as a function of distance;
• x equals distance.

Example

Example question: What is the amount of work done on a spring when it is compressed from its natural length of 1 m to a length of 0.75 m if the spring constant (stiffness of the spring) is k = 16 N/m? 

This is a good example since a spring requires increasing levels of work as it becomes more compressed.

Note that the spring compresses from its natural length of 1 m to 0.75 m, a distance of 0.25 m from the natural length. The lower limit is therefore 0 and the upper limit is .25.  Plug the values into the second formula:

Step 1: Calculate the indefinite integral:
16x dx = 8x² + C

Step 2: Compute the top boundary. For this example, that’s 0.25:
16x dx = 8*(0.25*0.25) = 0.5

Step 3: Compute the bottom boundary. For this example, that’s 0:
16x dx = 8*(0*0) = 0

Step 4: Subtract Step 3 from Step 2:
0.5 – 0 = 0.5

The amount of work required to compress the spring is 0.5 Newton-meters.

Work by Integration

Work by Integration is the computation of a constant or non-linear force applied over a distance between two points.

In physics, work done on a defined path is the force applied over the distance from one reference point to another. Written as the function W = Fx, simplified work accounts for a constant force that is applied on a straight path.

To account for forces occurring on paths not linear, an integral applied to the work equation takes the form:

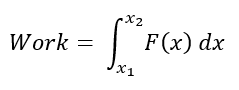
Where any work is done on a specified system is accounted for on whatever complex path the force F(x) is applied to over the interval [x₁,x₂]. The force function F(x) can be directly substituted for any relevant force function that is established by theory, such as the Spring Force Equation ½kx² or Coulomb’s Law of (kq₁q₂)/(r²).

Accounting for Force Variations

Since force is understood in Physics as a vector, there are cases where the force applied over a path may not always point at the path’s direction. Remember that vectors are defined with a magnitude and direction. A visual for this scenario is shown below, where the force direction is angled (θ) off from the path itself.

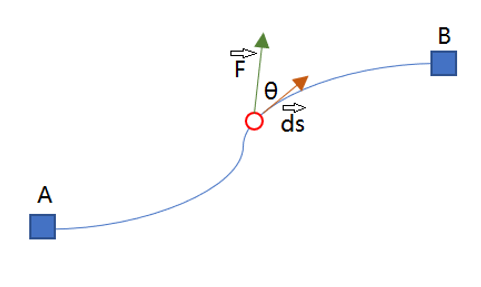
Work by integration can take the angling of the force into account by taking the integral of a scalar product between the force vector and path vector:

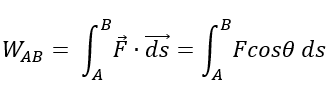
Where the cosine of the angle, between both vectors on the path interval [A, B] is present. Work is in its fullest for forces that are directly applied to the path taken (Rochester, 2014). Forces that angle off from the set path by 90 degrees equate to zero work via cos(90*) = 0. Two vector elements being perpendicular to each other is understood as both elements being independent of each other.

Pulley Example

A simple example that uses the integral is for a pulley system. Let’s say that a pulley for radius 1.5 meters is built to lift cargo that has a max weight limit of 150 kg. For the cargo to be lifted up 10 meters, how much for does the pulley exert? Assume that the pulley and rope to be massless.

Step 1: Determine if the force in this system is angled off from the path the cargo takes when lifted.

It can be safely assumed that the cargo being lifted upwards does not have a reflection angle from the string.

Step 2: Substitute for values within the equation and evaluate the integral over the lifting distance of 10 meters.

The distance traveled by the pulley is 2πr = (2π)(1.5) = 3π meters and F(x) = m*g

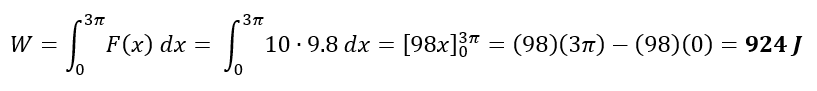
Work By Integration: Charged Particles Example

The work integral formula can be done for the distance that extends into the realm of infinity. When finding the work to put two opposite poled particles near each other, the force path consists of:

• The distance R we put both particles at.
• The infinite distance the particles slow down at to not have those particles exerting a force on each other.

For two protons, we can derive the work formula to pushing two protons next to each other. Given the Coulomb’s Law of (kq₁q₂)/(r²), where k is the proportionality constant equaling to 9e9 Nm²C^-2, the equation is formed as:

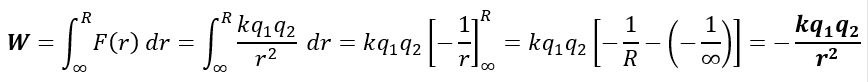
An intuitive shortcut could have been made that skips the integration step entirely. Since the force equation for two charged particles was given and that work is simply the force over a distance, then Coulomb’s Law over the distance R makes sense.

The negative direction for work presents a unique idea for the work’s direction. This example had work to be put into the system for the particles to be distanced R away from each other. If the particles were to be let go, the particles would exert that exact work value once they are infinite distance units apart.

Pumping Work Example

Pumping a liquid out a tank from the bottom can have its work calculated through the integral method discussed. An efficient approach to this problem is to consider the level drops for the liquid in a tank to be represented as small three-dimensional discs being dropped down.

For a cylindrical tank, disks of water can be imagined being lowered as the tank empties of its content. If a 10-meter-tall tank of radius 3 meters was asked to be drained of its water, how much work must a pump exert?

Step 1: Find the force equation for dropping infinitesimal units of water inside the tank’s dimensions.

Force = Density * Disc Area * Disk Height

Force = ρ * πr² * (H – x),   where H is the initial height of the water

Step 2: Substitute in the evaluated force equation into the work integral and solve for the work value. Consider the distance the water takes when dropping its water level.

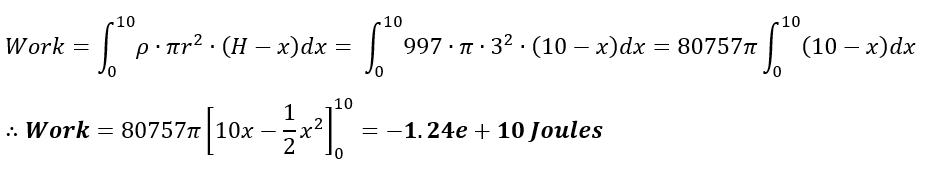
Reference

“Work by Integration.” Academic Success Center, Rochester Institute of Technology, 12 Sept. 2014, www.rit.edu/studentaffairs/asc/sites/rit.edu.studentaffairs.asc/files/docs/services/resources/handouts/C9_WorkbyIntegration_BP_9_22_14.pdf.