Series Convergence Tests Contents (Click to skip to that section):
Series Convergence Tests in Alphabetical Order
Often, you’ll want to know whether a series converges (i.e. reaches a certain number) or diverges (does not converge). Figuring this out from scratch can be an extremely difficult task —something that’s beyond the scope of even a calculus II course. Thankfully, mathematicians before you have calculated Series Convergence Tests: the convergence or divergence of many common series. This enables you to figure out whether a particular series may or may not converge.
Abel’s Test
Abel’s test is a convergence test for infinite series; It tells us whether some infinite series converges in certain situations.
More info: Abel’s test.
Absolute Convergence
If the absolute value of the series
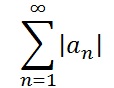
converges, then the series
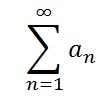
converges.
Alternating Series Convergence Tests
If for all n, an is positive, non-increasing (i.e. 0 < = an) and approaches 0, then the alternating series test tells us that the following alternating series converges:
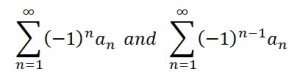
If the series converges, then the remainder R,sub>N = S – SN is bounded by |R N|< = aN + 1. S is the exact sum of the infinite series and SN is the sum of the first N terms of the series.
Deleting the first N Terms
The following series either both converge or both diverge if N is a positive integer.
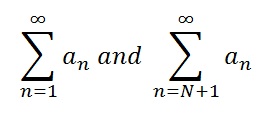
Series Convergence Tests: Dirichlet’s Test
Dirichlet’s test is a generalization of the alternating series test.
Dirichlet’s test is one way to determine if an infinite series converges to a finite value. The test is named after 19th-century German mathematician Peter Gustav Lejeune Dirichlet.
Formally, Dirichlet’s test states that the infinite series
a1b1 + a2b2 + … + anbn converges if the following two statements are true:
- The sequence of partial sums
sn = a1 + a2 + … an
is a bounded sequence. In other words, there is a positive number K so that
Sn < K for all n. - b1 + b2 + … bn is a monotonic decreasing sequence (i.e. a steadily decreasing sequence) converging to zero (i.e. bn < bn-1 and limn→∞) bn = 0).
When to Use Dirichlet’s Test
Dirichlet’s test is one of the lesser known tests. In general, the common rules for convergence of series—the ones you learn in elementary calculus—suffice for testing the vast majority of series. But there are some specific cases where the “usual” tests just don’t work.
For example, you can use the ratio test or root test to show that the following power series diverges (for |z|> 1) or converges absolutely for |z| < 1.
![]()
However, neither of those tests tell you what happens when z = 1. For that, you can use Dirichlet’s test to show that the series converges (Evans, 2009).
Example of Dirichlet’s Test
Use Dirichlet’s test to show that the following series converges:
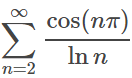
Step 1: Rewrite the series into the form a1b1 + a2b2 + … + anbn:
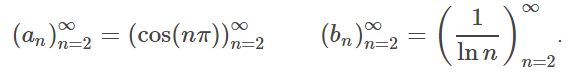
Step 2: Show that the sequence of partial sums an is bounded. One way to tackle this to to evaluate the first few sums and see if there is a trend:
- a2 = cos(2π) = 1
- a3 = cos(2π) + cos(3π) = 1 – 1 = 0
- a4 = cos(π) + cos(2π) + cos(3π) = 1 – 1 + 1 = 0
It appears the sequence of partial sums is bounded (≤1).
Step 3:Evaluate bn to see if it decreasing. One way to do this is to graph the function (I used Desmos.com):
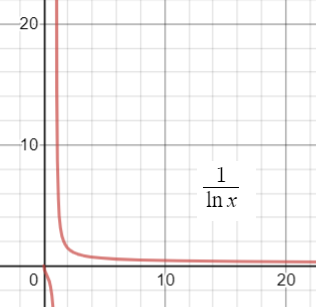
Clearly, the function (and therefore the sequence) is decreasing and the limit as n→∞ is 0. Therefore, this series converges.
Proof of Dirchlet’s Test
Watch the following video for a proof of convergence using Dirchlet’s test:
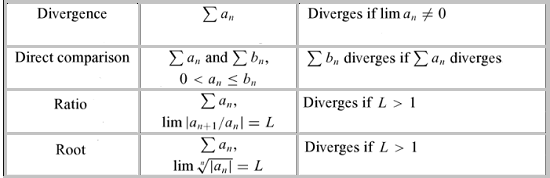
Direct Comparison Test
In the direct comparison test, the following two rules apply if 0 < = an < ;= bn for all n greater than some positive integer N.
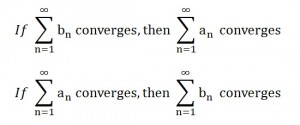
Geometric Series Convergence Tests
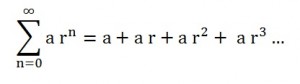
With the geometric series, if r is between -1 and 1 then the series converges to 1⁄(1 – r).
Integral Series Convergence Tests
The following series either both converge or both diverge if, for all n> = 1, f(n) = an and f is positive, continuous and decreasing. If the series does converge, then the remainder RN is bounded by
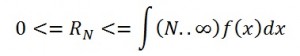
See: Integral Series / Remainder Estimate.
Limit Comparison Test
The limit comparison test states that the following series either both converge or both diverge if lim(N → ∞) (an⁄bn where an,bn>0 and L is positive and finite.
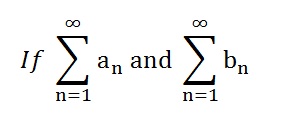
nth-Term Test for Divergence
The following series diverges if the sequence {an} doesn’t converge to 0:
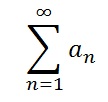
For several examples, see: Nth Term Test for Divergence.
P series
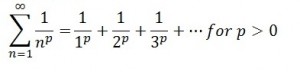
If p > 1, then the p-series converges.
If 0 < p < 1 then the series diverges.
Ratio Test
The following rules apply if for all n, n≠0. L = lim (n→ ∞)|an + 1⁄an|.
If L<1, then the series
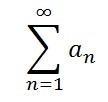
converges.
If L>1, then the series
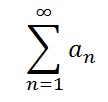
diverges.
If L = 1, then the ratio test is inconclusive.
More info: Ratio Test
Root Test
The root test tells us whether or not a series converges absolutely.
As its name suggests, it involves taking a root, and so it is most useful for exponential series and in situations where taking a root is quick and simple.
Determining Absolute Convergence Using the Root Test
To use the root test on a series:
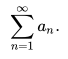
First, calculate the limit:
![]()
- If that limit is less than one, the series converges absolutely.
- If it is greater than one, it diverges.
- And if the limit is just one, we don’t know. It might converge conditionally, it might diverge.
There are other tests which can be used to determine convergence when the root test gives us an indeterminate answer.
Examples of the Root Test
To see how this works, suppose you are given the series:
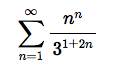
We need to take the limit, as n goes to infinity, of the nth root of that. Taking the nth root divides any exponent by 1/n. In the above formula, there are two exponents (n in the numerator and 1 + 2n in the denominator); each of these needs to be divided by 1/n.
Using that information, you should get:
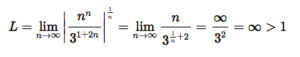
Since infinity is greater than 1, this series is divergent.
The following series is a little more interesting:
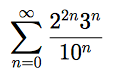
Here, again, we divide the exponents by 1/n.
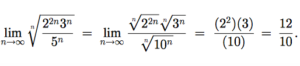
Since 12/10 is also greater than one, this series also diverges.
References
Belk, Jim. Math 142 Course Notes. Root Test. Bard College Math Department. Published Online Fall 2009. Retrieved from http://faculty.bard.edu/belk/math142af09/RootTest.pdf on August 26, 2019.
Oregon State Calculus Quest. Retrieved from https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/SandS/SeriesTests/root.html on August 26, 2019
Taylor Series Convergence
The Taylor series converges if f has derivatives of all orders on an interval “I” centered at c, if lim(n→ infin;)RN = 0 for all x in l:
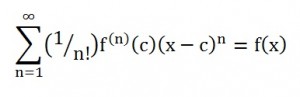
The Taylor series remainder of RN = S – SN is equal to (1/(n + 1)!)f(n + 1)(z)(x – c)n + 1 where z is a constant between x and c.
What Does “Converge” Mean?
Converge means to settle on a certain number. For example, the series {9, 5, 1, 0, 0, 0} has settled, or converged, on the number 0.
Integrals, limits, series and sequences can all converge. For example, if a limit settles on a certain (finite) number, then the limit exists. The opposite is diverge, where the integral, limit, series or sequence fails to settle on a number. In the case of a limit, if it diverges, then it doesn’t exist.
What Does Diverge Mean?
“Diverge” generally means either:
- Settles on a certain number (i.e. has a limit), or
- Doesn’t converge.
In some areas of math, diverge might simply mean “takes a different path” (for example, in KL Divergence in statistics). However, in calculus, it almost always pertains to limits or behavior of sequences and series.
Series and Sequences that Diverge (The Divergence Test)
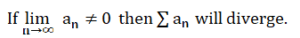
Series and Sequences can also diverge. In a general sense, diverge means that the sequence or series doesn’t settle on a particular number.
A divergent series will (usually) go on and on to infinity (i.e. these series don’t have limits). For example, the series
9 + 11 + 13 …
will keep on growing forever.
Not all series diverge though: some diverge all the time, others converge or diverge under very specific circumstances. For example:
- Series that diverge all the time include every infinite arithmetic series and the harmonic series.
- Series that sometimes converge include the power series, which converges everywhere or at a single point (outside of which the series will diverge).
Proving divergence (or convergence) is extremely challenging with a few exceptions. For example, you can show that an infinite series diverges by showing that a sequence of partial sums diverges.
Series Convergence Tests: Related Articles
Series Convergence Tests: References
Arfken, G. (1985). Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press.
Boas, R. et al. (1996). A Primer of Real Functions. Cambridge University Press.
Browder, A. (1996). Mathematical Analysis: An Introduction. New York: Springer-Verlag, 1996.
Clapham, C. & Nicholson, J. (2014). The Concise Oxford Dictionary of Mathematics. OUP Oxford.
Evans, P. (2009). Math 140A Test 2. Retrieved September 18, 2020 from: http://math.ucsd.edu/~lni/math140/math140a_Midterm_Sample2.pdf
Hunter, K. Sequences and Series of Functions.
Jeffreys, H. and Jeffreys, B. S. (1988). “Uniform Convergence of Sequences and Series” et seq. §1.112-1.1155 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 37-43, 1988.
Kadak, U. (2014). On Uniform Convergence of Sequences and Series of Fuzzy-Valued Functions. Retrieved February 10, 2020 from: https://www.hindawi.com/journals/jfs/2015/870179/
Kevrekidis, P. 132class13 (PDF). Retrieved December 14, 2018 from: http://people.math.umass.edu/~kevrekid/132_f10/132class13.pdf
Knopp, K. “Uniform Convergence.” §18 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 71-73, 1996.
Kuratowski, K. (2014). Introduction to Calculus. Elsevier.
Mathonline. Dirichlet’s Test for Convergence of Series of Real Numbers Examples 1. Retrieved September 18, 2020 from: http://mathonline.wikidot.com/dirichlet-s-test-for-convergence-examples-1
Nelson, D. (2008). The Penguin Dictionary of Mathematics. Penguin Books Limited.
Rudin, W. (1976). Principles of Mathematical Analysis, 3rd ed. New York: McGraw-Hill, pp. 147-148.
Spivak, M. (2006). Calculus, 3rd edition. Cambridge University Press.
Vasishtha, A. Algebra & Trigonometry.
Vogel, T. Pointwise and Uniform Convergence of Sequences of Functions (7.1). Retrieved February 10, 2020 from: https://www.math.tamu.edu/~tvogel/410/sect71a.pdf
Wood, A. (2012) Absolute and Conditional Convergence. Retrieved December 14, 2018 from: https://resources.saylor.org/wwwresources/archived/site/wp-content/uploads/2012/09/MA102-5.4.6-Absolute-and-Conditional-Convergence.pdf
Infographic based on Professor Joe Kahlig’s original graphic.