Contents:
Related article: Finite Geometric sequences.
What is a Geometric Series?
A geometric series (or geometric progression) is one where every two successive terms have the same ratio. Once a common factor is removed from the series, you end up with a value raised to a series of consecutive powers. This type of series have important applications in many fields, including economics, computer science, and physics.
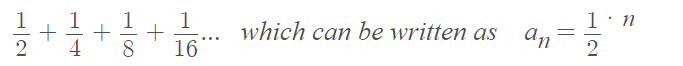
An infinite series is the description of an operation where infinitely many quantities, one after another, are added to a given starting quantity. Any geometric series can be written as
a + ar + ar2 + ar3 + …
where a is the initial term (also called the leading term) and r is the ratio that is constant between terms. We call this ratio the common ratio.
A geometric series can either be finite or infinite.
Finite Geometric Series
A finite geometric series has a set number of terms. For example, instead of having an infinite number of terms, it might have 10, 20, or 99. As long as there’s a set end to the series, then it’s finite. For example, all of the following are finite geometric series:
| Geometric Series | Starting Term (a) | Ratio (r) | Number of terms (n) |
| 2 + 4 + 8 + 16 + 32 | 2 | 2 | 5 |
| 2 – 20 + 200 – 2000 | 3 | -10 | 4 |
| 5 | ½ | 101 |
Infinite Geometric Series
The series:
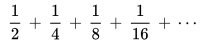
is an infinite geometric series. The “…” at the end of the series means that this particular series goes on to infinity. Each term is equal to the previous term times a constant, the common ratio. Since this common ratio is ½, we know this series converges, and we know it will approach (½)/(1 – ½) = 1 as the number of terms goes to infinity.
Another example of a this type of series is
2 + 4 + 8 + 16 + 32 + …,
Here again each term is equal to the previous term times a constant, so we know our series is geometric. The constant, 2, is greater than 1, so the series will diverge.
Alternating Geometric Series
The alternating geometric series has terms that alternate in sign: either the odd terms are negative or the even terms are negative. For example, the following series has odd terms that are negative [1]:
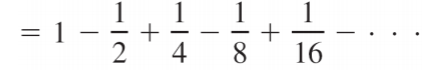
And this series has even terms that are negative:
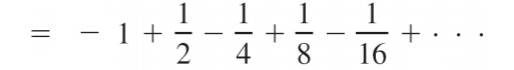
The alternating geometric series can also be written in summation notation. For example [2]:
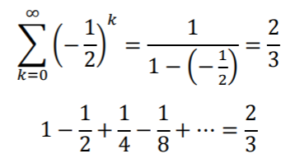
Convergence of an Alternating Geometric Series
An alternating geometric series will converge if its terms consistently get smaller and approach zero. Any series of this type with a small common ratio will rapidly converge. Therefore, you only need to sum a few terms.
Not all alternating geometric series will converge. To test convergence, use the alternating series test.
However, if
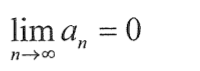
then use the nth term test instead.
Convergence in the Complex Plane
Alternating geometric series are either ascending or descending. The following table shows the conditions for convergence in the complex plane [3]:
| Case | Ascending | Descending |
| Divergent | |z| > 1 | |z| < 1 |
| Divergent | |z| = -1 | |z| = -1 |
| Oscillating | |z| = 1 ≠ -z | |z| = 1 ≠ -z |
| Absolutely Convergent | |z| < 1 | |z| > 1 |
| Totally Convergent | |z| ≤ 1 -ε | |z| ≥ 1 + δ |
| Where | 0 < ε < 1 | δ > 0 |
References
[1] Larson, R. et al. (1995). Calculus of a Single Variable: Early Transcendental Functions. Chapter 9. Infinite Series. Cengage Learning. Retrieved April 5, 2021 from: http://www.math.utep.edu/Faculty/nsharma/public_html/LarCalc10_ch09_sec5.pdf
[2] Hassoun, M. ECE 4330 Lecture 3 Math Review (Continued). Retrieved April 5, 2021 from: https://neuron.eng.wayne.edu/auth/ece4330/lectures/lecture_3_ece4330t.pdf
[3] Braga da Costa Campos, L. (2010). Complex Analysis with Applications to Flows and Fields. CRC Press.
Sum of a Convergent Geometric Series
The sum of a convergent geometric series can be calculated with the formula a⁄1 – r, where “a” is the first term in the series and “r” is the number getting raised to a power. A geometric series converges if the r-value (i.e. the number getting raised to a power) is between -1 and 1.
A geometric series
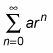
converges if and only if the absolute value of the common ratio, |r|, is less than 1. As a formula, that’s if:
0 < | r | < 1
Where r is the common ratio.
In this case, the series will approach a / (1 – r).
If the absolute value of r is greater or equal to 1, the series diverges. As a formula, that’s if:
| r | ≥ 1
In general, computing the sums of series in calculus is extremely difficult and is beyond the scope of a calculus II course. However, the geometric series is an exception.
Sum of a Convergent Geometric Series: Example
Example problem: Find the sum of the following geometric series:
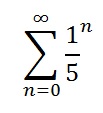
Step 1: Identify the r-value (the number getting raised to the power). In this sample problem, the r-value is 1⁄5.
Step 2: Confirm that the series actually converges. The r-value for this particular series ( 1⁄5) is between -1 and 1 so the series does converge.
Step 3: Find the first term. Get the first term by plugging the bottom “n” value from the summation. The bottom n-value is 0, so the first term in the series will be (1⁄5)0.
Step 4: Set up the formula to calculate the sum of the geometric series, a⁄1-r. “a” is the first term you calculated in Step 3 and “r” is the r-value from Step 1:
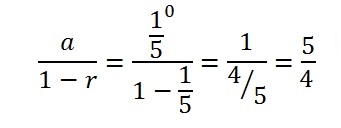
The sum of this particular geometric series is 5⁄4
That’s it!
What is the rth Moment?
A “rth moment” refers to the following geometric series:
The rth moment = (x1r + x2r + x3r +… + xnr) / n.
See: Rth moments and moments defined
References
Aomoto, K. & Kita, M. (2011). Theory of Hypergeometric Functions. Springer Science and Business Media.
Berresford, G. & Rocket, A. (2015). Applied Calculus. Cengage Learning.
Callahan, J. (2010). Advanced Calculus: A Geometric View. Springer Science & Business Media.
Erdelyi, A. Ed. (1955). Higher Transcendental Functions. McGraw-Hill.
Pearson, J. et al. (2017) Numerical methods for the computation of the confluent and Gauss hypergeometric functions. Numer Algor (2017) 74:821–866
Seaborn. Hypergeometric Functions and Their Applications. Retrieved November 26, 2019 from: https://books.google.com/books?id=HJXkBwAAQBAJ