A sequence of partial sums of the series S is a sequence where each term is the nth partial sum of S. In simple terms, in allows you to work with infinite sums (e.g. 1 + 2 + … ∞), which would be impossible to evaluate without some kind of cutoff point. However, where a sequence of partial sums is really important is because of what it tells us about its parent sequence.
Unpacking a Sequence of Partial Sums
The following example works through an example of why sequences of partial sums are so important.
A finite series is given by the terms of a finite sequence, added together. For example, take a look at the finite sequence:
![]()
For this particular sequence, the series would be:
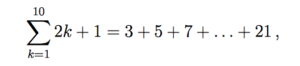
An infinite sequence is one that goes on to infinity, like this one:
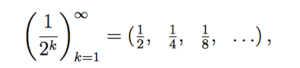
The series for that particular infinite sequence would be:
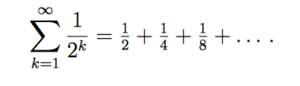
There’s no end to this summation; it goes on forever. That’s why we need partial sums: the sum of the first n terms in the series. This is what is called the “nth partial sum”. For example, the first 5 terms (5th partial sum), the first 287 terms (287th partial sum).
So we can make a new sequence, then, of all the partial sums. Call each term in our sequence ak, and the then we have.
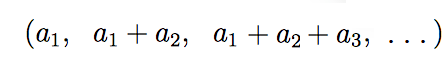
This sequence is very interesting because if it has a limit, we may say that the original infinite series has a sum. If it doesn’t have a real limit, we know that the series doesn’t have a sum.
Simple Example
As an example, let’s look at the infinite series
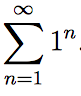
The partial sums here are:
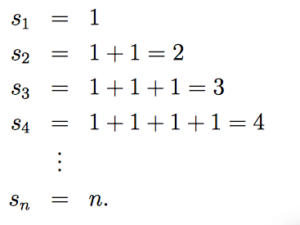
The sequence of these partial sums diverges, so we know that our original infinite series also diverges.
References
Math Centre. The sum of an Infinite Series. Published 2009, Retrieved from http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-convergence-2009-1.pdf on September 7, 2019
Texas Instruments. Module 23, Sequence and Series. Retrieved from https://education.ti.com/html/t3_free_courses/calculus84_online/mod23/mod23_lesson2.html on September 7, 2019.
Lahodny, Glenn Jr. Math 152 Class Notes: Section 10.2: Series. Retrieved from https://www.math.tamu.edu/~glahodny/Math152/Section%2010.2.pdf on September 7, 2019