Weierstrass M-Test: Definition
The Weierstrass M-Test is a convergence test that attempts to prove whether an infinite series is uniformly convergent and absolutely convergent on a set interval [xn, xm].
Let Mn(x) represent a nonnegative sequence of real numbers of n terms such that the summation of all terms in Mn is less than infinity. For a sequence Fn(x) consisting of real-valued functions or complex-valued functions on the interval [x1, x2], if the following inequalities hold true:
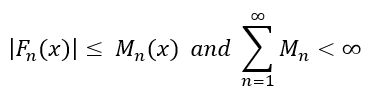
Then the sequence Fn(x) converges uniformly on the interval [x1, x2]. With the series of Fn(x) converging uniformly, it too converges absolutely without a condition needing to be set. The sum s(x) :
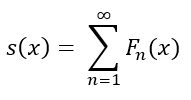
Becomes defined for all x within the closed interval [x1, x2]. For each n term in Mn(x), the Weierstrass M-Test must be held true for the convergence properties to exist on Fn(x).
Weierstrass M-Test Proof
Convergence tests such as the M-Test follows the similar purpose of using Direct Comparison or Limit Comparison Tests (Ringstrom, 2011). If a larger summation, acting as the upper bound to Fn(x), converges, then series like Fn(x) and smaller must converge due to comparison.
In similar footsteps to comparison testing, we denote the summation of a series by:
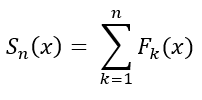
Where Sn(x) is the sum of n-terms for F(x). Then for m < n terms, we can set an equality for the difference of two sums based on how many terms were added up:
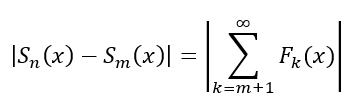
Pay attention to where the values m and n are located. Since we set m to be always less than n, the sum Sk(x) is set to add terms k = 1 to k = n. The sum Sk(x) for when m is implemented will always be a smaller interval since now the sum adds terms k = 1 to k = m. More terms are added up within Sn(x), thus Sn(x) has its terms k = 1 to k = m cut off and be changed to represent terms k = m + 1 to k = n.
The absolute value bars can be absorbed around sequence Fk(x) to change the equality into an inequality of less than or equals to.
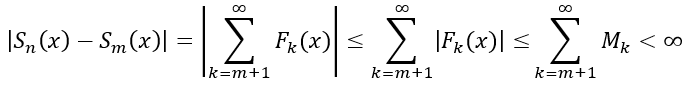
We can replace the symbol representation of the absolute of sequence Fk(x) with Mk. We know that the absolute difference between two sums should be less than infinity. Letting the sum of Mk be less than infinity carries on that property.
The focus then goes on proving Mk to converge from other available tests, like the Ratio Test or the P-Series Test.
The Big Picture from the Proof
If m gets large enough and still be less than n, then the tested Mk represents the right-end portion of the original series h(x) for its m + 1 to n terms. The larger the m-value, the more precise the evaluation becomes on the right-most terms. Imagine as though you are telescoping the last few terms for their behavior on converging to one number.
If the terms m+1 to n can get proven to converge, then the remaining portion of terms k = 1 to k = m must be helping the m + 1 to n terms to converge.
Limitation of the M-Test
Notice that the definition of the M-Test only has the potential to prove a series (in question) is uniformly convergent.
This test cannot be used to show that a chosen series does not uniformly converge.
Since the sequence Mn(x) chosen to test for Fn(x) does not depend on the convergence for x values, it is possible to have chosen Mn(x) whose series does not converge but the individual terms do converge. One can still use a non-convergent sequence Mn(x) and conclude Fn(x) to being uniformly convergent.
Practice Problem
For a given power series below, show that F(x) uniformly converges for the radius of convergence spanning [-1, 1].
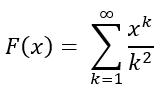
Step 1: An appropriate Mn(x) must be determined where all its terms are larger or equal to the terms in F(x).
For a function G(x) that is F(x) ≤ G(x), G(x) = k-2 can be used within the interval [-1, 1].
Step 2: Choose a series test to determine that Mn(x) converges and conclude the converge of F(x) by the Weierstrass M-Test.
The P-Series Test states that for sequences in the form 1/kp, the sequence converges if p>1.
Since p = 2 > 1, then G(x) converges and by the Weierstrass M-Test, F(x) converges uniformly and absolutely.
References
Ringstrom, Hans. “A BRIEF INTRODUCTION TO UNIFORM CONVERGENCE.” Department of Mathematics, KTH Royal Institute of Technology, 2011, www.math.kth.se/math/GRU/2010.2011/SF1629/CTFYS/uniform.pdf.