Integral Test: Definition
The Integral Test is used to prove whether a sequence an or its corresponding function f(x) converges or not; It is defined by approaching a given series of partial sums through integration.
Integral Test Formulation
The test begins by finding a function f(n) that, for the half-closed interval [1, ∞), contains three properties:
- A continuous function,
- All positive values,
- The function is decreasing.
Equating f(n) = an for all n ≥ N, where both n and N are positive integers, forces both the summation of an and the integral of f(x) to either converge or diverge.
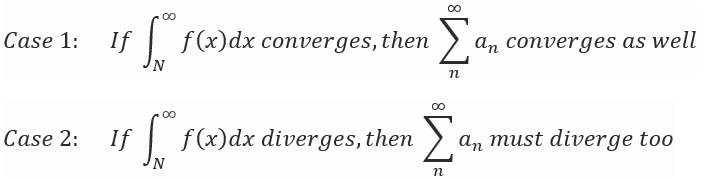 The integral needs to be evaluated first to have the sequence in question follow suit in the determination of convergence or divergence. If the sequence an has its representing function f(x) decrease in value as the step size n increases, then—as n goes to infinity—the y-value for f(x) equals zero. Therefore, the sum of all y-values from n = 1 to n = N will conclude the convergence property of an.
The integral needs to be evaluated first to have the sequence in question follow suit in the determination of convergence or divergence. If the sequence an has its representing function f(x) decrease in value as the step size n increases, then—as n goes to infinity—the y-value for f(x) equals zero. Therefore, the sum of all y-values from n = 1 to n = N will conclude the convergence property of an.
The integral test is only used to determine if the given sequence an converges, but never for the sequence’s converging value. There isn’t a process that can evaluate a given series for its exact converging value.
The reasoning is that the integral itself captures the area underneath its curve while the summation of a sequence takes the sum of y-values produced by f(x) for each iteration of n. This issue is solved through the Remainder Estimation in addition to the logical solving procedure below.
Integral Test Remainder
For f(x) that contains the properties of being continuous, positive, and decreasing for x ≥ no and for the sequence an to being able to converge, an Upper Bound and Lower Bound exists that act as a remainder. The remainder value represents the error when approximating the infinite summation of an to the nth partial sum. Since the integral test can’t determine the exact value for the summation of an, there will always be a positive non-zero remainder when performing an approximation attempt.
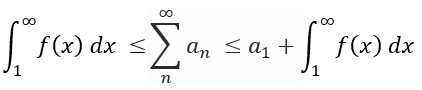
Limitations on the Upper and Lower Bounds for the value of the sequence an can be represented as:
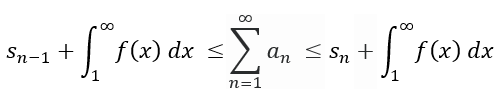
Where:
- sn – 1 represents the summation for an for one term less than what n was set for originally and
- sn represents the summation for an for n terms.
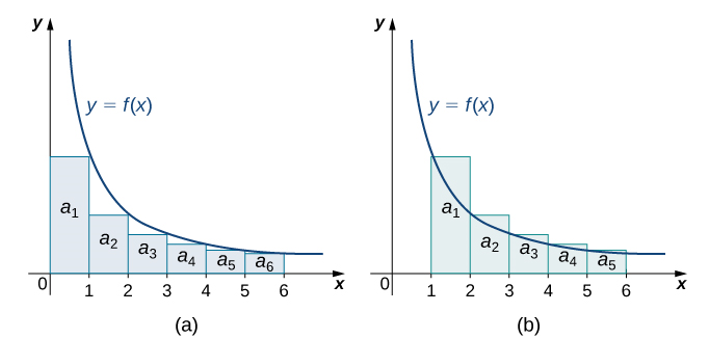
The first inequality group can be represented by two visuals. Graph (a) has the function f(x) being integrated above the rectangles that the summation for an is accounting for. Graph (b) has the same function f(x) being integrated below the rectangles that the summation for an is accounting for (UT Calculus).
The second inequality group represents the underestimation that comes from sn alone and can be added to the integral of f(x) to obtain the smallest possible converging value for the sequence an.
Estimation Example
A typical series to evaluate can be done for a p-series: an = n-2. We would like to approximate the sequence’s converging value to three decimal places.
Step 1: Set up the summation to then evaluate the integral within the Integral Test.
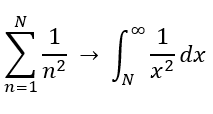
For an approximation of three decimal places, we limit the integral to have a ceiling of 1/1000 in error.
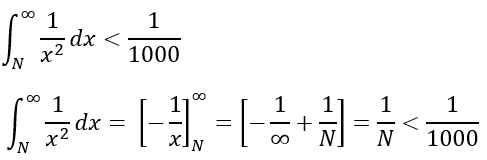
Step 2: Attempt a value N to determine if N needs to be increased to reduce the error of concluding two approximations.
For N-1 < 1/1000, the first attempt for a N value can be N = 1000
Then the lower approximation equates to:
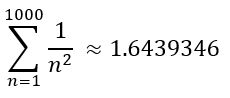
And the upper approximation equates to:
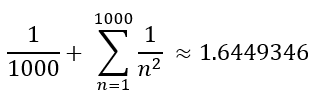
The current conclusion rests between the sum equaling to either 1.644 or 1.645. Thus, N needs to be larger to have the sum settling on a single number with three decimal places.
Step 3: If the requested decimal rounding rests between two values, increase the N value to reevaluate the series converging approximation.
Since the difference in error between the two approximations is ± 0.0005, we can focus on finding N where N-1 = 0.00025. In this case, N = 4000 and the two approximations can be reevaluated.
The new lower approximation equates to:
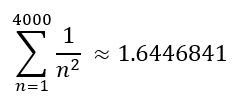
And the new upper approximation equates to:
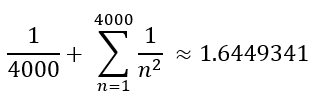
Both values, rounded to three decimals, equate to the same value of 1.645.
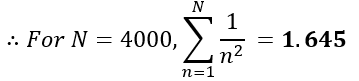
Reference
“Estimates of Value of the Series.” UT Calculus, web.ma.utexas.edu/users/m408s/m408d/CurrentWeb/LM11-3-5.php.