Contents:
Harmonic Series
The harmonic series is defined as:
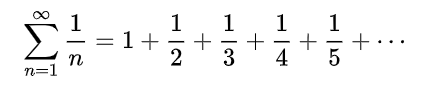
Each term of the series, except the first, is the harmonic mean of its neighbors.
The harmonic series is widely used in calculus and physics. It is a special case of the p-series, which has the form:
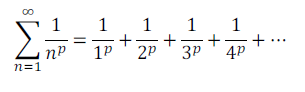
When p = 1, the p-series becomes the harmonic series.
Divergence of the Harmonic Series
The harmonic series diverges . This seems strange, considering the terms eventually get smaller and smaller, diminishing to zero. However, you can prove in a few different ways that is does in fact, diverge.
First, the partial sums grow without limit. That said, it takes a very long time for the sequence to grow: it takes in excess of 1043 terms to reach a sum of 100 (Thompson & Gardner, 2014).
One proof was first formulated by Nicole Oresme (1323–1382). The proof, which you can still find in textbooks today, involves grouping terms as follows:
![]()
Each group has 1, 1, 2, 4, 8, 16… terms, and the sum of each group is at least ½. Therefore, this shows that the series diverges.
The integral test can be used to show divergence.
History of the Harmonic Series
Mathematicians developed the series based on musical notes: terms in the series were developed as fractions of the fundamental frequency in music (the lowest resonant frequency of a musical instrument). For example, ½ is twice the fundamental frequency and ⅓ is three times the fundamental frequency. The origins of the harmonic series go back as far as Pythagoras, who studied music as an abstract science (Larson & Edwards, 2008).
Alternating Harmonic Series
The alternating harmonic series is the sum:
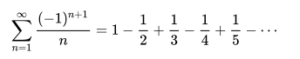
Which converges (i.e. settles on a certain number) to ln(2). It is the x = 1 case of the Mercator series, and also a special case of the Dirichlet eta function.
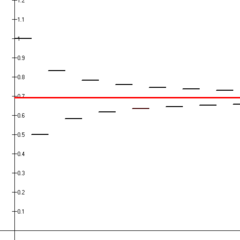
The image below shows the first fourteen partial sums of this series. Ln(2) is shown in red. The more terms of the sequence are added up, the closer we get to the line ln(2). With a large number of terms, the difference is indistinguishable.
The harmonic series and alternating harmonic series both get their names from the harmonic wavelengths of music, which follow the same pattern.
Conditional Convergence of the Alternating Harmonic Series
It’s important to note that although the alternating harmonic series does converge to ln 2, it only converges conditionally. It is not absolutely convergent, for it is possible to rearrange the terms of the series so that we can come up with any answer whatsoever.
Assume, for example, you wanted it to converge to 2.0. Then you could sum a few positive terms, to get something slightly greater than 2. Add one negative term, so that the sum is just below 2; then add enough positive terms to make it go above 2 again. Continue doing this, going closer and closer to 2, and if you repeat forever—as you can, since you have an infinite number of terms—it will converge to 2.

References
Chung, K. 8. Fundamental frequency and harmonics.
Harrison. Lecture 2, Sequences and Series. Retrieved from https://www.ch.ic.ac.uk/harrison/Teaching/L2_Seq-Series-2.pdf on August 21, 2019
Hudleson, Matt. Proof Without Words. Mathematics Magazine 83 (2010) 294. doi:10.4169/002557010X521831. Mathematical Association of America. Retrieved from https://www.maa.org/sites/default/files/Hudleson-MMz-201007804.pdf on August 21, 2019
Larson, R. & Edwards, B. (2008). Calculus of a Single Variable. Cengage Learning.
Thompson,S. & Gardner, M. (2014). Calculus Made Easy. St. Martin’s Publishing Group.
The Harmonic Divergence. (2007). MAA Minicourse, San Jose MathFest. Retrieved February 5, 2020 from: https://www.macalester.edu/~bressoud/talks/mathfest2007/harmonicproblems.pdf