Calculus Definitions > Gamma Function
Contents (Click to skip to that section):
- What is the Gamma Function?
- Incomplete Gamma Function
- Multivariate Gamma Function
- Double Gamma (Barnes G) Function
- Digamma (Psi) Function
- Log Gamma Function
- Polygamma Function
What is the Gamma Function?
The Gamma function (sometimes called the Euler Gamma function) is the following improper integral:
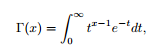
This definition is related to factorials (the product of an integer and all the integers below it; e.g. factorial three (3!) is equal to 3 * 2 * 1 = 12) by the following formula:
Γ(n) = (x – 1)!.
While the factorial function is only defined for non-negative integers, gamma can handle fractions as well as complex numbers.
For positive values x < 1. the integrand becomes infinitely large as t approaches 0.
For values of x greater than or equal to 1, it is a convergent series.
Interesting Note: The Mathematical Association of America has a scan of Euler’s original 1938 work on the function. You can find it here.
In Excel
In Microsoft Excel, the Function (which uses the above definition) is:
GAMMA(number)
For values of 0 or less, GAMMA will return an error (#NUM!).
Alternate Definition
A second, similar, definition is:
![]()
Notation
The notation Γ(n) = (x – 1)! is due to the mathematician Legendre. It is the most common form for the function.
Equivalent, rarely used, versions of the formula include:
- Π (n) = n! (from
- (z – 1)!.
Particular Values for the Gamma Function
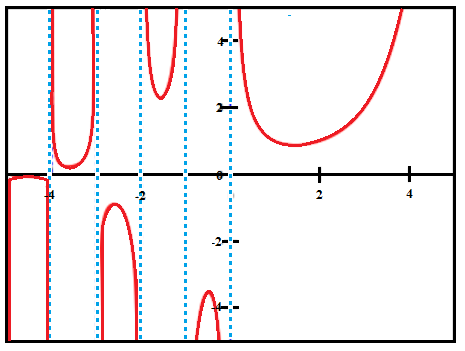
Particular values include:
- Γ(-1) = (-1 – 1)! = -2! = ∞.
- Γ(0) = (0 – 1)! = -1! = ∞.
- Γ(1/2) = (1/2 – 1)! = -1/2! = √π.
- Γ(1) = (1 – 1)! = 0! = 1.
- Γ(4) = (4 – 1)! = 3 x 2 x 1 = 6.
Any whole negative number leads to a value of infinity, while any positive whole number leads to a value of 1. This is one of the strange results the formula is famous for. The function is also well known in probability for the result Γ(1/2) = √π.
Incomplete Gamma Function
While the gamma function (a.k.a. the “complete” gamma function) is defined as an integral from zero to infinity, the incomplete gamma function is defined from zero to a variable upper limit (the lower incomplete gamma function) or from a variable lower limit to infinity (the upper incomplete gamma function). The upper incomplete gamma function is sometimes called the complementary incomplete gamma function or Prym’s function, after 19th century German mathematician Friedrich Prym.
The incomplete gamma function and the complementary incomplete gamma function are usually defined by the following integrals [1]:
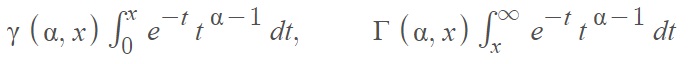
It’s common to see analytical series representations of the function, especially in physics and engineering. For example, the following asymptotic series can be used to estimate Γ for large values of x [2]:
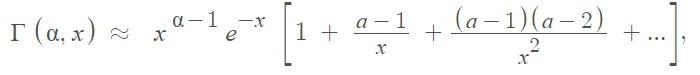
You may come across normalized and non-normalized versions:
- Normalized versions (regularized incomplete gamma functions) have a range of [0, 1]. These are usually encountered in statistical applications.
- Non-normalized versions have a range of [0, Γ(a)].
Multivariate Gamma Function
The multivariate gamma function (MGF) is an extension of the gamma function for multiple variables. While the gamma function can only handle one input (“x”), the multivariate version can handle many. It is usually defined as:
Where:
- ? = the space of m x m real, positive definite (and hence matrices,
- dS = product Lebesgue measure of ½p(p + 1) distinct elements in S.
The Multivariate Gamma can also be written as a product of gamma functions as follows (Muirhead, 2009):
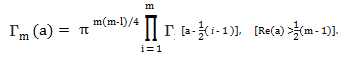
When m = 1, we drop the m in Γm(a), so the equation simply becomes the gamma function Γ(a). You may also see the notation Γd(x), although this particular notation also denotes the incomplete regular gamma in some texts (Gentle, 2007).
Applications of the Multivariate Gamma Function
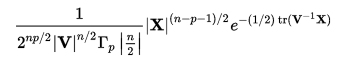
The MGF has no real practical application but it is used extensively in multivariate statistical analysis. For example, the MGF is included in the probability density function of the Wishart distribution, which is an important part of Bayesian Psychometric Modeling, Signal Processing and many other sub-fields of multivariate analysis. The MGF is also used to derive the general form of the generalized multivariate gamma distribution’s probability distribution function (PDF).
Note: A positive definite matrix is a symmetric matrix with all positive eigenvalues. Eigenvalues are special scalars; When you multiply a matrix by a vector and get the same vector as an answer, along with a new scalar, the scalar is called an eigenvalue.
Barnes G Function
The Barnes G-Function (also called the Double Gamma function or simply the G-function), is a generalization of the Gamma function. It is used in many areas of mathematics (e.g. random matrix theory and analytic number theory) and theoretical physics.
It has a few equivalent forms including (for example) the following definition as an entire function in the complex plane (Adamchik, 2001):
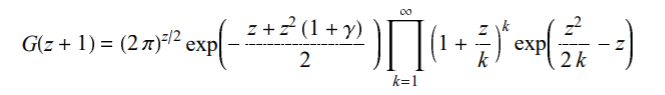
Where:
- γ is the Euler-Mascheroni constant,
- exp(x) = ex,
- Π – capital pi.
History of the Barnes G-Function
Barnes G-Function, or simply the G-function, was first described by Barnes in 1900. He described it as
“… substantially the simplest transcendental integral function with zeros at the points
z = -nω, n = 1, 2, … ∞;
the zero at the point z = -nω being of order n.
Other authors, like Alexeiewsky and Holder had previously touched on the G-function, but their papers were more concerned with quotients involving the function rather than the function itself.
G-Function and Gamma Function
The Barnes G Function is an extension of the gamma function and shares many similar properties. For example, both functions satisfy the same kind of functional equation G (z + 1) = Γ(z) G(z). With an initial value of G(1) = 1, it’s possible to find values for G for all integers (Benjamin & Brown, 2009).
Both functions also satisfy the following multiplication formula (Adamchik, 2005):
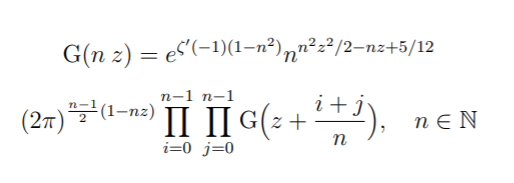
Digamma Function
The digamma function is a special function that is the logarithmic derivative of the gamma function. Multiple differentiations of the digamma function lead to polygamma functions (Oldham et al. 2010).
Pairman (1919) named the function after digamma (ϝ), an archaic letter of the Greek alphabet. However, that notation soon fell out of favor, perhaps because of it’s similarity to the “f” in function notation. The usual symbol for the digamma function is the Greek letter psi(ψ), so the digamma is sometimes called the psi function.
The digamma function appears in the definition of Bessel functions of the second kind and has many applications in computing and number theory. For example, the function is useful for calculating infinite rational sums. The digamma function is meromorphic with simple poles at z = 0, -1, -2, -3, … (Chaudry & Zubair, 2001).
Digamma Function Definition
The digamma function is traditionally defined as the derivative of the logarithm of the gamma function (rather than the derivative of the function itself). In other words, obtain the gamma function, take its logarithm, then find the derivative of that logarithmic function. This is perhaps the simplest way to evaluate the function, although there are a number of other ways. In fact, the function has a variety of integral and series representations (Coffey, 2010).
Perhaps the most well know representation of the digamma function is (Azose, 2016) :
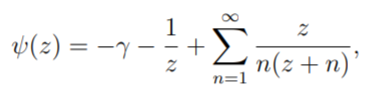
Another common definition (Chaudry & Zubair, 2007):
![]()
However, it can also be defined in terms of limits:
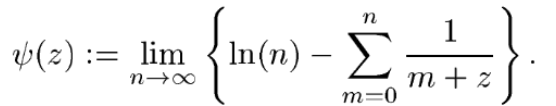
Alternatively, it can be represented by the series:
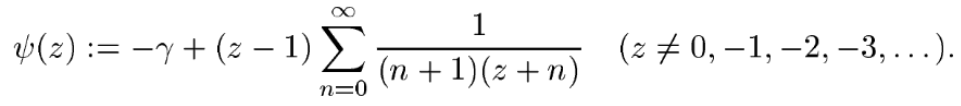
Log Gamma Function
The log gamma function is the logarithm of the gamma function. It grows more slowly than the gamma function, making it an ideal choice for graphing, wave propagation, and in computer applications to avoid overflow.
One of the more common ways to define the function is:
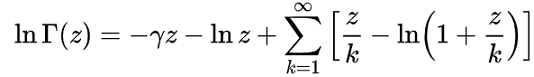
There are various equivalents, including (for complex variable z):
ln γ(z) – ln γ(z + 1) – ln z
The complex-variabled function is meromorphic on ℂ and holomorphic on ℂ \ ℝ- ∪ 0 (Gullerud, 2017), where ℂ = the set of complex numbers and ℝ = the set of real numbers.
Derivatives of The Log Gamma Function
The derivative of the log gamma function is the digamma function (Abramowitz and Stegun (1965, p. 258.). The second derivative is the trigamma function, third is tetragamma and fourth is pentagamma; Higher derivatives are called polygamma functions.
This online calculator from Casio calculates the log gamma function with a high degree of accuracy.
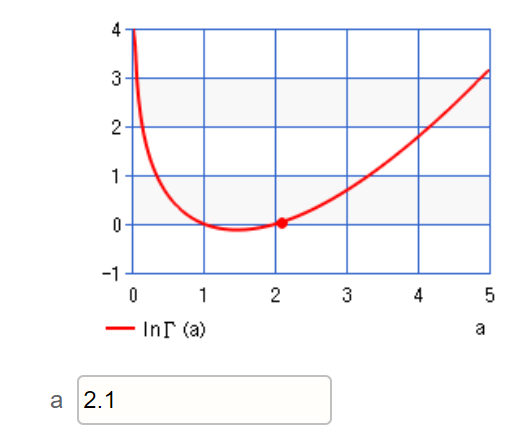
Log Gamma Distribution
A log gamma distribution for some random variable X has a probability density function of:
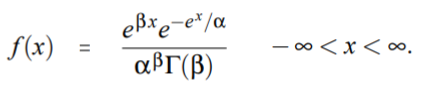
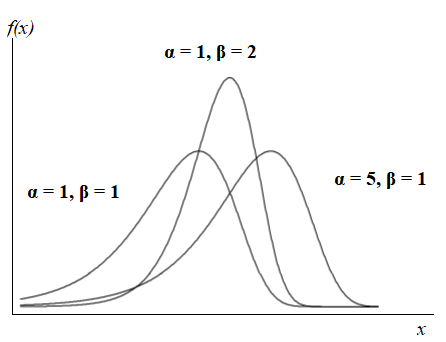
The positive scale parameter α and positive shape parameter β control the shape of the graph. The scale parameter usually “squeezes” the graph from the left and right as though the graph was in a vise; The shape parameter affects the overall shape of the graph. The following graph shows the PDF for three different parameter combinations:
Polygamma Function
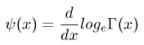
The polygamma function is a special function intimately related to the gamma function. It can be represented by ψ0(z) or Fm(z).
All polygamma functions resemble the digamma function in the following ways (Oldham, 2009):
- Monotonic for positive arguments,
- Segmented for negative arguments,
- Discontinuities at all nonpositive integer arguments.
Relation of the Polygamma Function to Other Functions
The polygamma function is the nth derivative of the Gamma function (Bonnar, 2017). In other words, every polygamma is a higher order derivative of the gamma function. For example:
- First derivative: Trigamma function,
- Second derivative: Tetragamma function,
- Third derivative: Pentagamma function,
- Fourth derivative: Hexagamma function
The polygamma can also be defined as the logarithmic derivative of the gamma function— the (k + 1)th derivative of the loggamma function (Cuyt et al, 2008):
![]()
Mathematica Notes
In Mathematica, Polygamma[z] is equal to digamma[z]. The nth derivative of digamma[z] is PolyGamma[n, z] (Wolfram, 1996).
References
[1] Gautschi, R. A computational Procedure for Incomplete Gamma Functions. Retrieved July 3, 2021 from: https://www.cs.purdue.edu/homes/wxg/selected_works/section_02/068.pdf
[2] Amore, P. Asymptotic and exact series representations for the incomplete Gamma function. Retrieved July 3, 2021 from: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.341.1492&rep=rep1&type=pdf
Abramowitz, M., and Stegun, I. A. (Eds.). (1965). Handbook of Mathematical Functions. New York: Dover.
Adamchik, V. (2001). On the Barnes Function. Retrieved April 20, 2020 from: http://www.cs.cmu.edu/~adamchik/articles/issac/issac01.pdf
Adamchik, V. (2005). Symbolic and Numeric Computations of the Barnes Function. Retrieved April 20, 2020 from: https://www.cs.cmu.edu/~adamchik/articles/PhysCom.pdf
Alexeiewsky, “Ueber die Functionene welche der Gamma Functionen ahnlich sind. Annales de l’ Imp. Univ. de Charkow, 1889.
Arfken, G. “Digamma and Polygamma Functions.” §10.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 549-555, 1985.
Azose, J. (2016). On the Gamma Function and its Applications. University of Washington.
Bonnar, J. (2017). The Gamma Function. Treasure Trove of Mathematics from: https://www.google.com/books/edition/The_Gamma_Function/qJ_QDwAAQBAJ?hl=en&gbpv=0&kptab=getbook
Burns, P. (1998). S Poetry. TIBCO.
Chau, K. (2017). Theory of Differential Equations in Engineering and Mechanics. CRC Press.
Chaudry, M. & Zubair, S. (2001). On a Class of Incomplete Gamma Functions with Applications. CRC Press.
Coffey, M. (2001). Integral and series representations of the digamma and polygamma functions. Retrieved August 26, 2020 from: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.741.4749&rep=rep1&type=pdf
Cuyt, A. et al. (2008). Handbook of Continued Fractions for Special Functions. Springer Netherlands.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, 2007.
Barnes, E. (1900) The Theory of the G-Function. In The Quarterly Journal of Pure and Applied Mathematics.
Bateman, H & Erdélyi, A. (1955) “Higher Transcendental Functions” [in 3 volumes]. Mc Graw-Hill Book Company.
Benjamin, A. & Brown, E. (1990). Biscuits of Number Theory. Mathematical Association of America.
Boros, G. and Moll, V. “The Expansion of the Loggamma Function.” §10.6 in Irresistible Integrals: Symbolics, Analysis and Experiments in the Evaluation of Integrals. Cambridge, England: Cambridge University Press, pp. 201-203, 2004.
Davis, P. J. (1959). “Leonhard Euler’s Integral”, The American Mathematical Monthly, Vol. 66, No. 10 (Dec., 1959), pp. 849–869.
Das & Dey (2007). On Bayesian Inference for Generalized Multivariate Gamma Distribution.
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, 1981.
Gentle, J. (2007). Matrix Algebra: Theory, Computations, and Applications in Statistics. Springer Science & Business Media.
Gullerud, M. (2017). The Gamma Function. Retrieved August 8, 2020 from:
Leemis, L. (2020). Loggamma. Retrieved August 8, 2020 from: https://people.uwec.edu/mbirika/M395_Riemann/gamma-function.pdf http://www.math.wm.edu/~leemis/chart/UDR/PDFs/Loggamma.pdf
Oldham, K. et al. (2010). An Atlas of Functions. With Equator, the Atlas Function Calculator. Springer New York.
Pairman, E. (1919) Tables of Digamma and Trigamma Functions. In Tracts for Computers, No. 1, K. Pearson (Ed.),
Sloane, N. J. A. Sequences A075700 and A102887 in “The On-Line Encyclopedia of Integer Sequences.”
Wang & Li (2011) “Efficient Gaussian Graphical Model Determination without Approximating Normalizing Constant of the G-Wishart distribution ” http://www.stat.sc.edu/~wang345/RESEARCH/GWishart/GWishart.html
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.Muirhead (2009). Aspects of Multivariate Statistical Theory. John Wiley and Sons.
Wolfram, S. (1996). The Mathematica Book. Wolfram Research, Chicago.
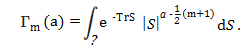
Is there any way in Excel to calculate the incomplete upper gamma function for negative shape factor (alpha) and positive x?
This isn’t one that I’ve used. I did find a few tips here: https://www.pcreview.co.uk/threads/excel-add-ins-incomplete-gamma-function.1757156/. Hope that helps!