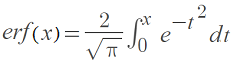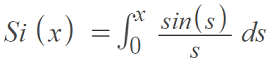In calculus, “Integral Function” can refer to one of two things:
- Another name for an antiderivative,
- A software function (e.g. on the TI-89) that performs integration.
Mathematical Integral Function
An “integration function”, with the symbol ∫, is usually just another name for an antiderivative [1].
An integration function can be given specific values which go from point a to point b on a graph, usually (but not always) along the x-axis. These “integral bounds” allow us to calculate the area under a specific segment of graph from x = a to x = b. For example, the integral function
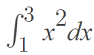
calculates the area under the curve of f(x) = x2 from x = 1 to x = 3:
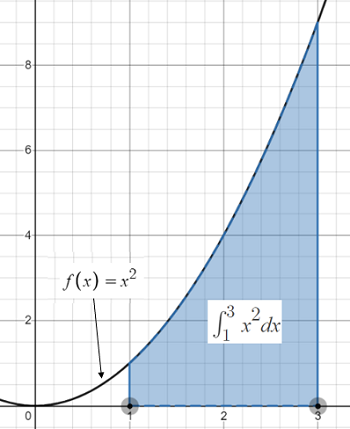
When the integral function is used to calculate an area for a specific section of a graph, it’s called a definite integral.
When we talk about integration, the “function” part is usually dropped. So we calculate an integral, rather than work with an integral function. An exception is in the fundamental theorem of calculus, where the “integral function” is frequently mentioned to make it clear that the reciprocal behavior of integrals and derivatives is a functional relationship.
Named Integral Functions
Some integral functions have been used so often that workers in some fields have “named” them and tabulated their values. These well known functions, popular in certain fields like engineering and physics, include [2]:
- The error function erf

- The sine integral function (used in electrical engineering) Si

Software Integral Functions
An integral function performs integration using software.
For example, in MATLAB, The calling syntax is:
I = integral(@function_name,lower,upper)
The function f(x) = erx can be integrated with [3]:
function[y] = = integ1(x,r)
y = exp (r*x);
For step by step instructions for the TI 89 integral function, see: TI-89 Integrals.
References
Graph: Desmos graphing calculator.
[1] Indefinite Integrals and Antiderivatives. Retrieved April 26, 2021 from: https://web.ma.utexas.edu/users/m408n/m408c/CurrentWeb/LM5-4-2.php
[2] Integration and Differential Equations. Retrieved April 26, 2021 from: http://howellkb.uah.edu/public_html/DEtext/Part1/Integration.pdf
[3] Little, L. More On Definite Integrals. Retrieved April 26, 2021 from: http://www.cps.brockport.edu/~little/CLASSES/F2020/ESC251/NOTES/Integration_2.pdf