The relative rate of change (RROC) is the ratio of a function’s derivative to itself.
The RROC of y = f(t) at t = a is defined as [1]:
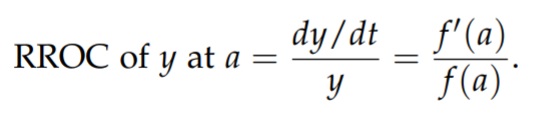
Relative rates of change are often expressed as the percentage change of y per unit change in x; for example, if the amount in an investment increases in value from $1000 to $1400 dollars over ten years, then the amount increases at an average rate of 4 percent per year during that ten-year interval.
Relative Rate of Change: Examples
Example question #1: What is the relative rate of change of f(x) = x3 at x = 4?
Solution: The derivative of f(x) = x3 is 3x2 (using the power rule), so:
RROC = f′(4) / f(4) = 3 * 42 / 43 = 48 / 64 = 3/4
Example question #2: Corn production in the U.S., C = f(t), in millions of tones, is a function of t years since the beginning of 2010. If f(8) = 253 and f′(8) = 17, what is the RROC of C at t = 8? Interpret it in terms of corn production.
Solution: RROC = f′(8) / f(8) = 17/253 ≈ 0.0672 = 6.72%
In 2018, corn production in the U.S. grew by 6.72% per year.
Example question #2: Annual world production of photovoltaic (PV) cells, S, in megawatts, is approximated by S = 277e0.368t, where t is years since 2000. Estimate the RROC of PV cell production in 2010 using Δt = 1.
Solution:
We’re told that S = 277e0.368t is an estimate.
We’re given Δt = 1, we have to format the RROC equation to include that fact.
Step 1: Find the derivative at t = 10 (i.e. 2010):
f′(10) = f(11) – f(10) / 11 – 10 = 277e0.368(11) – 277e0.368(10) / 1
= 15867.33 – 10982.05
= 4885.28.
Step 2: Find RROC. We already know f(10) from Step 1, so:
RROC = f′(10) / f(10)
= 4885.28 / 10982.05
= .44484 or 44.484%.
References
[1] Math 124. 2: Rate of Change: The derivative. Retrieved July 3, 2021 from: https://users.math.msu.edu/users/liuqinbo/chapter2.pdf