Unusual Probability Distributions (You’ve Never Heard of)

Copy

Probability distributions > Unusual Probability Distributions

These unusual probability distributions (or unusual names for distributions) never made it to the mainstream. You won’t find these in your regular textbooks, but I did come across this interesting list put together by Prof. Shakti [1].

List of Unusual Probability Distributions

  1. The array distribution refers to the conditional distribution of independent random variables X1 (given X2, … ,Xn).
  2. The Arfwedsen distribution (the coupon-collecting distribution or Dixie cup) is a discrete probability distribution for an urn sampling problem for drawings without replacement. Specifically, it tackles the problem “An urn contains N numbered balls. We make n drawings replacing the ball into the urn each time. What is the probability of getting v different balls?”[2]
  3. Binomials Added Distribution: The problem of adding binomials was addressed briefly in [3], referencing a formula for a toric ideal. Otherwise, it seems to have disappeared into obscurity.
  4. Bipolar distribution: a specific type of bimodal distribution that has two distinct peaks offering contradictory information. In some cases, the term may also refer to the Watson bipolar distribution.
  5. The Bravais distribution is another name for the bivariate normal distribution, (also sometimes called the bivariate Gaussian or Bivariate Laplace–Gauss distribution).
  6. Chi-bar-squared distribution: a mixture of chi-square distributions, mixed over their degrees of freedom.
  7. Darmois-Koopman distribution (or Koopman-Darmois) is a member of the exponential-type class of probability distributions.
  8. The de Moivre distribution: another name for the normal distribution. The use of “de Moivre distribution” to describe the normal distribution is thought to originate with Freudenthal [4], who advocated the name because De Moivre was the first to define the distribution, in 1733 [5].
  9. The Elfving distribution is defined as
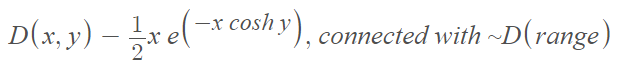
    unusual probability distributions

    The distribution is named after Finnish statistician and mathematician Gustav Elfving (1908-1984), who described the distribution in 1947.
  10. The exceedance distribution function (EDF) is defined as 1 minus the cumulative distribution function (CDF) [1]:

    EDF = 1 – CDF

References

[1] Shakti, P. (2022). P-Distribution. Retrieved March 15, 2022 from: https://p-distribution.com/probability-distributions-list/
[2] G. Arfwedson, A probability distribution connected with Stirling’s second class numbers. Skand. Aktuarietidskr. 34 (1951), 121–132.
[3] Carlini, E. & Rapallo, F. (2013). Toric ideals with linear components: an algebraic interpretation of clustering the cells of a contingency table.
[3] Freudenthal, H. (1966b). Waarschijnlijkheid en Statistiek [Probability and Statistics]. Haarlem: De Erven F. Bohn.
[4] Daw, R. & Pearson, E. Studies in the History of Probability and Statistics. XXX. Abraham De Moivre’s 1733 Derivation of the Normal Curve: A Bibliographical Note. Biometrika Vol. 59, No. 3 (Dec., 1972), pp. 677-680 (4 pages)
Oxford University Press


Comments? Need to post a correction? Please Contact Us.