Statistics Definitions > Univariate Analysis
What is Univariate Analysis?
Univariate analysis is the simplest form of analyzing data. “Uni” means “one”, so in other words your data has only one variable. It doesn’t deal with causes or relationships (unlike regression ) and it’s major purpose is to describe; It takes data, summarizes that data and finds patterns in the data.
What is a variable in Univariate Analysis?
A variable in univariate analysis is just a condition or subset that your data falls into. You can think of it as a “category.” For example, the analysis might look at a variable of “age” or it might look at “height” or “weight”. However, it doesn’t look at more than one variable at a time otherwise it becomes bivariate analysis (or in the case of 3 or more variables it would be called multivariate analysis).
The following frequency distribution table shows one variable (left column) and the count in the right column.
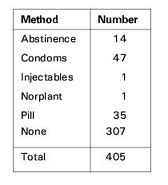
You could have more than one variable in the above chart. For example, you could add the variable “Location”or “Age” or something else, and make a separate column for location or age. In that case you would have bivariate data because you would then have two variables.
Univariate Descriptive Statistics
Some ways you can describe patterns found in univariate data include central tendency (mean, mode and median) and dispersion: range , variance, maximum, minimum, quartiles (including the interquartile range), and standard deviation.
You have several options for describing data with univariate data. Click on the link to find out more about each type of graph or chart:
Check out our Statistics YouTube channel for hundreds of videos on elementary statistics, probability and more.
References
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.