Contents:
- Quartiles: Definition, Finding
- What is an Upper Quartile?
- Quartile Function Excel
- Difference between a quarter and a quartile
What are Quartiles? Definition
Quartiles are values that divide your data into quarters. However, quartiles aren’t shaped like pizza slices; Instead they divide your data into four segments according to where the numbers fall on the number line. The four quarters that divide a data set into quartiles are:
- The lowest 25% of numbers.
- The next lowest 25% of numbers (up to the median).
- The second highest 25% of numbers (above the median).
- The highest 25% of numbers.

As quartiles divide numbers up according to where their position is on the number line, you have to put the numbers in order before you can figure out where the quartiles are.
Find Quartiles: Examples
Need help with a homework question? Check out our tutoring page!
Example: Divide the following data set into quartiles: 2, 5, 6, 7, 10, 22, 13, 14, 16, 65, 45, 12.
Step 1: Put the numbers in order: 2, 5, 6, 7, 10, 12 13, 14, 16, 22, 45, 65.
Step 2: Count how many numbers there are in your set and then divide by 4 to cut the list of numbers into quarters. There are 12 numbers in this set, so you would have 3 numbers in each quartile.
2, 5, 6, | 7, 10, 12 | 13, 14, 16, | 22, 45, 65
If you have an uneven set of numbers, it’s OK to slice a number down the middle. This can get a little tricky (imagine trying to divide 10, 13, 17, 19, 21 into quarters!), so you may want to use an online interquartile range calculator to figure those quartiles out for you. The calculator gives you the 25th Percentile, which is the end of the first quartile, the 50th Percentile which is the end of the second quartile (or the median) and the 75th Percentile, which is the end of the third quartile. For 10, 13, 17, 19 and 21 the results are:
25th Percentile: 11.5
50th Percentile: 17
75th Percentile: 20
Interquartile Range: 8.5.
Why do we need quartiles in statistics? The main reason is to perform further calculations, like the interquartile range, which is a measure of how the data is spread out around the mean.
What is an Upper Quartile?
The upper quartile (sometimes called Q3) is the number dividing the third and fourth quartile. The upper quartile can also be thought of as the median of the upper half of the numbers. The upper quartile is also called the 75th percentile; it splits the lowest 75% of data from the highest 25%.
Calculating the Upper Quartile
You can find the upper quartile by placing a set of numbers in order and working out Q3 by hand, or you can use the upper quartile formula. If you have a small set of numbers (under about 20), by hand is usually the easiest option. However, the formula works for all sets of numbers, from very small to very large. You may also want to use the formula if you are uncomfortable with finding the median for sets of data with odd or even numbers.
27, 19, 5, 7, 6, 9, 15, 12, 18, 2, 1.
By Hand
Step 1: Put your numbers in order: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27
Step 2: Find the median: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
Step 3: Place parentheses around the numbers above the median.
1, 2, 5, 6, 7, 9, (12, 15, 18, 19, 27).
Step 4: Find the median of the upper set of numbers. This is the upper quartile:
1, 2, 5, 6, 7, 9, (12, 15, 18 ,19 ,27).
Using the Formula
The upper quartile formula is:
Q3 = ¾(n + 1)th Term.
The formula doesn’t give you the value for the upper quartile, it gives you the place. For example, the 5th place, or the 76th place.
Step 1: Put your numbers in order: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
Note: for very large data sets, you may want to use Excel to place your numbers in order. See: Sorting Numbers in Excel.
Step 2: Work the formula. There are 11 numbers in the set, so:
Q3 = ¾(n + 1)th Term.
Q3 = ¾(11 + 1)th Term.
Q3 = ¾(12)th Term.
Q3 = 9th Term.
In this set of numbers (1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27), the upper quartile (18) is the 9th term, or the 9th place from the left.
Quartile Function Excel
You can also find a quartile in Microsoft Excel using the Excel quartile function.
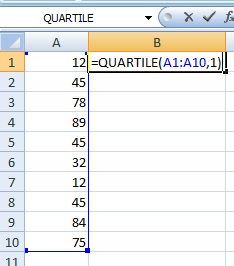
- Type your data into a single column. For example, type your data into cells A1 to A10.
- Click an empty cell somewhere on the sheet. For example, click cell B1.
- Type “=QUARTILE(A1:A10,1)” and then press “Enter”. This finds the first quartile. To find the third quartile, type “=QUARTILE(A1:A10,3)”.
Note: If your data is in a different cell range other than A1:A10, make sure you change the function to reflect that.
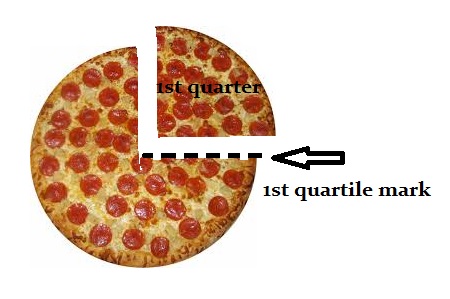
Difference between a quarter and a quartile
There’s a slight difference between a quarter and quartile. A quarter is the whole slice of pizza, but a quartile is the mark the pizza cutter makes at the end of the slice.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education