Estimator: Simple Definition and Examples

What is an Estimator?

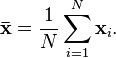
An estimator is a statistic that estimates some fact about the population. You can also think of an estimator as the rule that creates an estimate. For example, the sample mean(x̄) is an estimator for the population mean, μ.

The quantity that is being estimated (i.e. the one you want to know) is called the estimand. For example, let’s say you wanted to know the average height of children in a certain school with a population of 1000 students. You take a sample of 30 children, measure them and find that the mean height is 56 inches. This is your sample mean, the estimator. You use the sample mean to estimate that the population mean (your estimand) is about 56 inches.

Point vs. Interval

Estimators can be a range of values (like a confidence interval) or a single value (like the standard deviation). When an estimator is a range of values, it’s called an interval estimate. For the height example above, you might add on a confidence interval of a couple of inches either way, say 54 to 58 inches. When it is a single value — like 56 inches — it’s called a point estimate.

Types

Estimators can be described in several ways (click on the bold word for the main article on that term):

Biased: a statistic that is either an overestimate or an underestimate.
Efficient: a statistic with small variances (the one with the smallest possible variance is also called the “best”). Inefficient estimators can give you good results as well, but they usually requires much larger samples.
Invariant: statistics that are not easily changed by transformations, like simple data shifts.
Shrinkage: a raw estimate that’s improved by combining it with other information. See also: The James-Stein estimator.
Sufficient: a statistic that estimates the population parameter as well as if you knew all of the data in all possible samples.
Unbiased: an accurate statistic that neither underestimates nor overestimates.

Next: Estimating with the German Tank Problem.