Mixed Derivative (Partial, Iterated)

Derivatives >

The mixed derivative (also called a mixed partial derivative) is a second order derivative of a function of two or more variables. “Mixed” refers to whether the second derivative itself has two or more variables. For example:

• f_xy and f_yx are mixed,
• f_xx and f_yy are not mixed.

Mixed Derivative Example

The function of two variables f(x, y) can be differentiated with respect to x or y, giving two first order partial derivatives ∂f / ∂x and ∂f / ∂y. These can be differentiated again with respect to x and y, giving rise to four different second order derivatives:

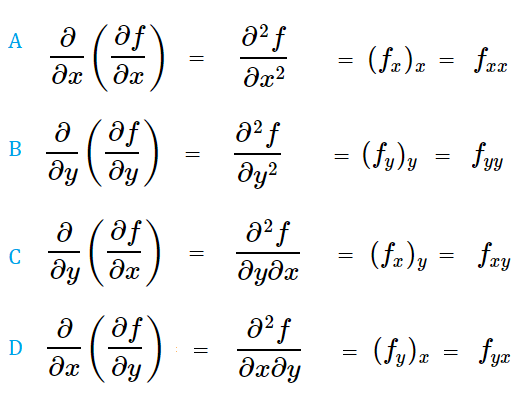
A and B are called “unmixed derivatives” because they contain the same variables (xx, yy); C and D are called “mixed derivatives”. Together, all four are iterated partial derivatives of second order.

The variable which appears first is generally the one you would want to differentiate with respect to first. For example, f_yx means that you should differentiate with respect to y, then differentiate with respect to x. However, if all the derivatives within the mixed derivatives are continuous, you can make a series of interchanges between x and y. For example, you could write them so that differentiations to x all come first, as in f_xyy or f_xxy (Brand, 2013).

Example question: Find the mixed derivatives of f(x, y) = x² y³.

Solution Steps:
Step 1: Find the first partial derivatives.

• With respect to x (holding y constant): f_x = 2xy³
• With respect to y (holding x constant): f_y = 3x²²

Note: The term “hold constant” means to leave that particular expression unchanged. In this example, “hold x constant” means to leave x² “as is.” Likewise, hold y constant means that you leave y³ as is.

Step 2: Find the second order derivatives. There are four:

• f_xx = 2y³
• f_xy = 6xy²
• f_yx = 6xy²
• f_xx = 6x²y

Step 3: Identify the mixed partial derivatives. There are two:

• f_xx = 2y³
• f_xy = 6xy²
• f_yx = 6xy²
• f_xx = 6x²y

Notation for Mixed Derivative

The curly d (∂) is usually used as notation for a mixed derivative. Other notations you might see (especially in older texts) include D₂xy^z and z_xy. For higher-order derivatives, f_xy′ is often used (Berry et al., 1989).

Note of Number of Indices

Technically, a mixed derivative refers to any partial derivative with two or more non-zero indices m_i. For example f(x, y, z) or f(g, h, k). However, functions of two variables are more common. In addition, listing mixed derivatives for functions of more than two variables can quickly become quite confusing to keep track of all the parts. While a function of two variables has four mixed partial derivatives, a function of three variables has 27 ! (xxx, xxy, xxz, xyy, xyz…).

References

Berry, J. et al. (1989). Introductory Mathematics Through Science Applications. Cambridge University Press.
Brand, L. (2013). Advanced Calculus: An Introduction to Classical Analysis. Dover Publications.
Newcastle University (2018). Partial Derivatives. Retrieved August 28, 2020 from: https://internal.ncl.ac.uk/ask/numeracy-maths-statistics/core-mathematics/calculus/partial-derivatives.html#:~:text=Second%20Order%20and%20Mixed%20Derivatives&text=The%20second%20order%20derivatives%20f,to%20more%20than%20one%20variable.
Tesler, P. (2018). Iterated Partial Derivatives. Retrieved August 28, 2020 from: https://www.math.ucsd.edu/~gptesler/20c/slides/20c_itderivs_f18-handout.pdf