A normalizing constant ensures that a probability density function has a probability of 1. The constant can take on various guises: it could be a scalar value, an equation, or even a function. As such, there isn’t a “one size fits all” constant; every probability distribution that doesn’t sum to 1 is going to have an individual normalization constant.
In many cases, the nonnormalized density function is known, but the normalization constant is not. In simple PDFs, the constant may be calculated relatively easy. In other cases, especially when the constant is a complicated function of the parameter space, it may be impossible to calculate.
Normalization Constant Examples
In a beta distribution, the function in the denominator of the pdf acts as a normalizing constant.
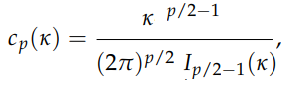
The normalizing constant in the Von Mises Fisher distribution is found by integrating polar coordinates.
In the Kent distribution, the normalizing constant is an equation:
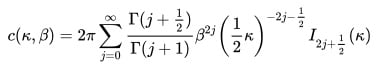
For Bayes’ rule, written as [1]:
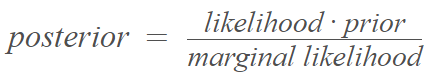
The denominator is the normalizing constant ensuring the posterior distribution adds up to 1; it can be calculated by summing the numerator over all possible values of the random variable. Calculation of the normalization becomes much more difficult for procedures like Bayes factor model selection or Bayesian model averaging; these are notoriously difficult to calculate and usually involve high dimensional integrals that are impossible to solve analytically [2].
References
[1] Murphy, K. In Symbols. Retrieved November 16, 2021 from: https://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html
[2] Gronau, Q. et al. bridgesampling: An R Package for Estimating Normalizing Constants. Retrieved November 16, 2021 from: https://cran.r-project.org/web/packages/bridgesampling/vignettes/bridgesampling_paper.pdf