Contents:
What is Inverse Probability?
Inverse probability is the probability of things that are unobserved; or, more technically, the probability distribution of an unobserved variable. It’s generally considered an obsolete term.
Nowadays, the basis of inverse probability (determining the unobserved variable) is usually called inferential statistics, and the main problem of inverse probability—finding a probability distribution for an unobserved variable—is usually called Bayesian probability.
Inverse Probability, aka Bayesian Probability— What it Involves
Bayesian probability is often used when we want to calculate the likelihood of certain outcomes given a particular hypothesis. It’s a way of making logical inference problems into simple statistics problems, by looking at conditional probabilities and comparing outcomes given different hypothetical scenarios.
The Bayes Rule formula is:
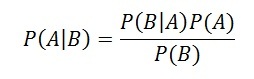
The rule can be written with slightly different notation to illustrate the connection between a hypothesis and a condition:
Here P(H|D) is the likelihood that hypothesis H is true given a particular condition D, P(D|H) is the probability that the condition D is true given the hypothesis being true, and P(H) and P(D) are the probabilities of observing the hypothesis and the condition D, independently of each other.
Watch the video for a quick example of working a Bayes’ Theorem problem, or read a different example problem below:
Simple Inverse Probability Example: Applying Bayes Rule
A screening test for a particular genetic abnormality is highly effective; it gives 99% true positive results for those who carry the abnormality, and 95% true negative results to those who don’t. Only a very small percentage of the general population, 0.001%, carry this genetic abnormality.
Inverse probability and Bayes rule allows us to calculate what the likelihood is that a random someone carries the genetic abnormality, given a positive test. The genetic abnormality is the hypothesis, and the positive test is our condition. In our formula above, we’ll want to plug in the values:
P(D|H) = 0.99
P(H) = 0.00001
P(D), or the probability of a positive test, is just the sum of two terms. The first term is the probability of a positive test given the genetic abnormality times the likelihood that the abnormality exists. The second term will be the probability of a positive test given no genetic abnormality, times the likelihood of no genetic abnormality. So:
P(D) = P(D|H) P(H) + P(D|~H) P(~H).
That equals 0.99*0.00001 + 0.01*0.99999, or 0.0100098.
Plugging these into the formula above for Bayes rule, we get:
P(H|D) = [0.99*0.00001] / 0.0100098
Or, with no regard for significant digits, 0.00098903074. We see that though the test may be fairly reliable, the genetic abnormality is rare enough that even a positive test only leaves a person with only about a 0.09 percent likelihood of having the abnormality.
What is an Inverse Distribution?
“Inverse distribution” is one of those terms that has several meanings, depending on where you’re reading about it. It’s one of those informal terms that means one thing if you’re working with sampling in statistics, another if you’re looking at cumulative distribution functions and yet another if the variables in a distribution are reciprocals. According to the Oxford Dictionary of Statistical Terms, the different definitions include:
- The reciprocal of a random variable’s probability distribution. For example, The inverse gamma distribution is the reciprocal of the gamma distribution.
- Sampling up to a certain number of successes. See: Inverse sampling.
- Distributions where frequencies are reciprocal quantities (e.g. the factorial distribution),
- As a way to find variables in terms of the distribution function F(x). For example, the inverse normal distribution refers to the technique of working backwards, given F(x) to find x-values.
While all definitions are valid uses of the term “Inverse Distribution”, the term “Inverse Distribution Function” usually implies definition #4, i.e. actually using it to find probabilities.
Next: Bayes Theorem Problems.
References
Olshausen, B. (2004). Bayesian Probability Theory. Retrieved December 5, 2017 from http://redwood.berkeley.edu/bruno/npb163/bayes.pdf.
Bayes Theorem, Stanford Encyclopedia of Philosophy
https://plato.stanford.edu/entries/bayes-theorem/