Parametrization: What Does it Mean to Parameterize?

Statistics Definitions > Parametrization

This article is about defining probability distributions using parameters. If you’re trying to find out about population parameters (covered in elementary statistics), see: What is a Parameter in Statistics?

What is Parametrization?

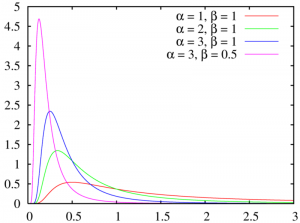
Simply put, parametrization (or parameterization) is where you change certain aspects a probability distribution by tweaking its parameters.

Many different parameters can be used to define a probability distribution. For example:

Normal distributions are parameterized by their mean (a location parameter) and standard deviation (a scale parameter).
The beta distribution has two positive shape parameters which control the shape of the distribution.
The gamma distribution has a shape parameter and a rate parameter.

More specifically, when you parametrize you specify a curve or shape with values in a specified range. Parametric families have many possible parameters; which you choose is usually a matter of convenience, simplicity, and usefulness (Breiman, 1973).

A More Formal Definition

A function can be used to represent parametrization. In fact, the function that defines a statistical model is sometimes called the model’s parameterization. The function is taken from a set θ with values in P so that θ → P^θ (Commenges, 2004). Notation is as follows:

P = family of probabilities,
Π = (P^θ; θ ∈ Θ)—A parametrization for a certain family of probabilities. Parametrizations of the same family of probabilities can be denoted with Π₁, Π₂…Π_n.

However, a function isn’t enough on its own to define a model. An identifiable model is one with known parameters and a set of random variables.

Frequentist vs. Bayesian Parametrization

In frequentist statistics, parametrization doesn’t change the probabilities in the model. It just changes the location on the number line, the general shape, or the spread. However, in Bayesian theory, it can lead to new priors and new models (Gelman, 2004).

References

Breiman, L. (1973). Statistics: with a view toward applications. Houghton Mifflin.
Commenges, D. (2009). Statistical models: Conventional, penalized and hierarchical likelihood. Statistics Surveys. Vol. 3 (2009) 1–17.
Gelman, A. (2004). Parameterization and Bayesian Modeling. Journal of the American Statistical Association. Volume 99, 2004 – Issue 466.