Population variance (σ2) tells us how data points in a specific population are spread out. It is the average of the distances from each data point in the population to the mean, squared.
σ2 is usually represented as σ2 and can be calculated using the following formula:
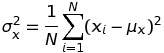
Here N is the population size and the xi are data points. μ is the population mean.
Example
Sample question: Find the population variance of the age of children in a family of five children aged 16, 11, 9, 8, and 1:
Step 1: Find the mean, μx:
μ = 9.
Step 2: Subtract each data point from the mean, then square the result:
(16-9)2 = 49
(11-9)2 = 4
(9-9)2 = 0
(8-9)2 = 1
(1-9)2 = 64.
Step 3: Add up all of the squared differences from Step 2:
(16-9)2 + (11-9)2 + (9-9)2 + (8-9)2+ (1-9)2 = 118.
Step 4: Divide Step 3 by the number of items. 118/5 gives a population variance of 23.6.
Properties of Population Variance
Since the population variance measures spread, σ2 for a set of identical points is 0.
If you add a constant to every data point the σ2 remains unchanged. For instance, suppose you study the birth years of senior citizens in New York and decide to switch calendars from the standard Gregorian one to a calendar where 1900 was year 1, the σ2 would stay the same.
The square root of the population variance is the population standard deviation, which represents the average distance from the mean.
The population variance is a parameter of the population, and is not dependent on research methods or sampling practices.
Differences Between Population Variance and Sample Variance
The sample variance is an estimate of σ2, and is very useful in situations where calculating the population variance would be too cumbersome. The only differences in the way the sample variance is calculated is that the sample mean is used, the deviations is summed up over the sample, and the sum is divided by n-1 (Why use n-1?). When calculating sample variance, n is the number of sample points (vs N for population size in the formula above).
Unlike the population variance, the sample variance is simply a statistic of the sample. It depends on research methodology and on the sample chosen. A new sample or a new experiment will likely give you a different sample variance, although if your samples are both representative your sample variances should be good estimates of the population variance and so close to each other.
Sources
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.