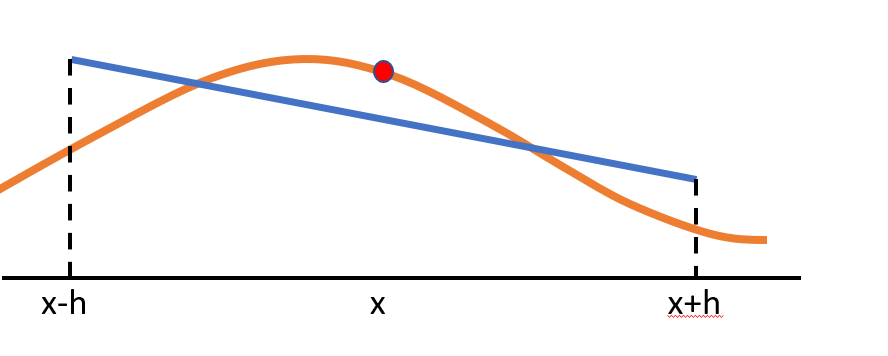
The Lanczos derivative (LD), named after Hungarian mathematician Cornelius Lanczos (pronounced Lan’tsosh), exists for many functions which fail to be differentiable using traditional methods or symmetric derivatives. This method, derived from the least squares model, can be thought of as the line of best fit on a symmetric interval centered at x [2].
Formal Definition of the Lanczos Derivative
the Lanczos derivative is defined in terms of a definite integral [1]:
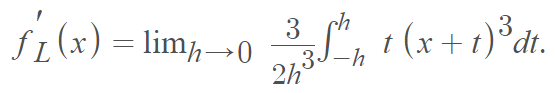
as long as the limit exists.
The method involves calculating the above expression for a small positive value of h. It is an extension of the ordinary derivative [2] and converges to the average of the left- and right-hand derivatives of a function. If both of these derivatives exist at a certain point x, then the LD will exist as well, even if there is a hole (a removable discontinuity) in the function at x.
Example
Example question: Find the Lanczos derivative of f(x) = x3.
Step 1: Place x3 into the formula:
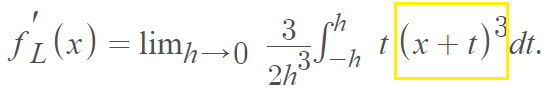
Step 2: Integrate:
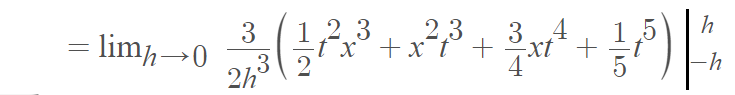
Step 3: Evaluate:
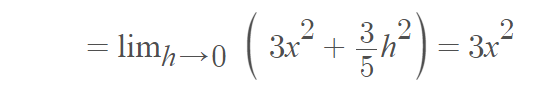
Advantages and Disadvantages of the Lanczos Derivative
One advantage to this method is that it allows us to find a “pseudo-derivative” for non-differentiable points. It can come in handy for numerical differentiation, especially when functions are not well-behaved like those with noise perturbations or functions given in sampled form [3]. Interestingly, the accuracy of the Lanczos derivative is superior to the accuracy of the ordinary derivative, which uses secant lines instead of the line of best fit.
One major disadvantage to the method is that the product rule, quotient rule, and chain rule all fail for the Lanczos derivative [4], which means that those shortcuts are not available. Therefore, it involves lengthy calculations which can quickly become very tedious.
References
[1] Washburn, L. The Lanczos Derivative. Retrieved August 10, 2021 from: https://www.whitman.edu/Documents/Academics/Mathematics/washbuea.pdf
[2] Liptaj, A. (2019). Maximal generalization of Lanczos’ derivative
using one-dimensional integrals. Retrieved August 10, 2021 from: https://arxiv.org/pdf/1906.04921.pdf
[3] Turuel, G. (2018). A New Class of Generalized Lanczos Derivatives. Palestine Journal of Mathematics. Vol 7(1), 211-221.
[4] Gordon, R. (2009/2010). A Least Squares Approach to Differentiation. Real. Anal. Exhange 35(1): 205-208.