What is a Symmetric Derivative?
A symmetric derivative exists for a function at a point if the following limit exists [1]:
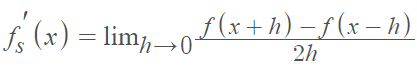
At first glance, this is very similar to the definition for the traditional derivative:
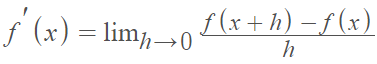
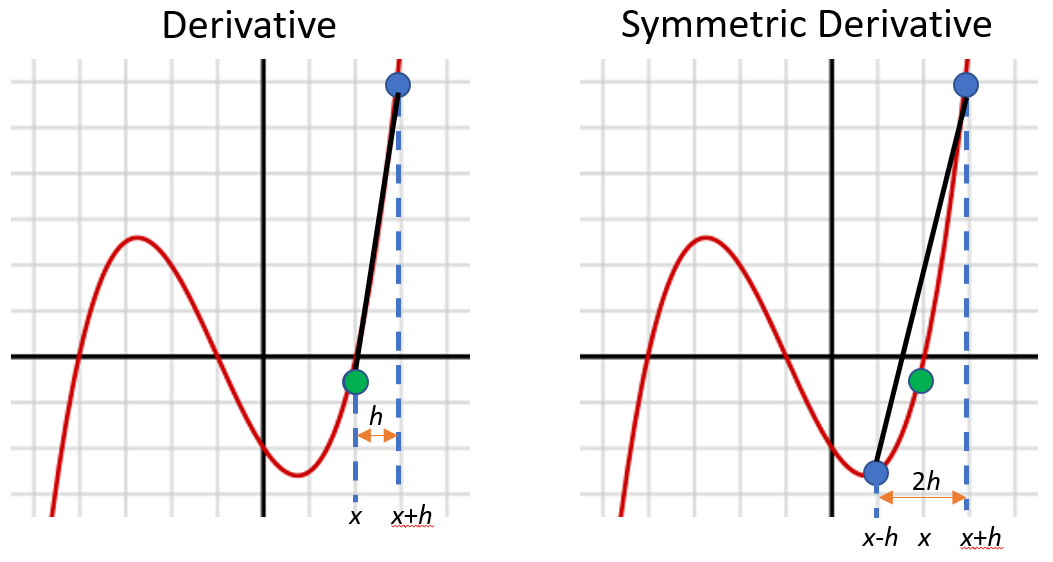
The main difference between the symmetric and traditional derivative is in the points used to calculate the slope [2]. The traditional derivative uses two points (x, f(x)) and (x + h, f(x + h)) to find the slope. This includes the point of interest, x. The symmetric derivative does not use x. Instead, it uses (x – h, f(x – h)) and (x + h, f(x + h)), which lie either side of x.
The symmetric derivative will always exist when the derivative of f exists in the traditional sense. However, the converse is not true. In some cases, the symmetric derivative exists when the traditional derivative does not. For example, the derivative of the absolute value function f(x) = |x| is undefined at x = 0. However, the symmetric derivative does exist:
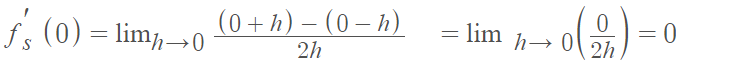
One benefit is that the symmetric type can deal with removable discontinuities (e.g. a hole at zero). However, this isn’t always a good thing. If a function behaves strangely near to a point, it may be counterbalanced by an equivalent strangeness on the other side. Therefore, you might get a perfectly reasonable looking solution that makes no practical sense at all.
When you’re dealing with basic functions, it probably doesn’t make much difference which formula you use (symmetric or traditional). If you know for sure that a function is differentiable at x, then you can use either the symmetric or traditional derivative. In some cases, it may be easier to use symmetric form, particularly when performing numerical differentiation on computers [4].
Sliding the Symmetric Derivative
“Sliding” the symmetric derivative by ½h (i.e. adding a constant multiple to every base point) turns the first symmetric derivative into an ordinary one:
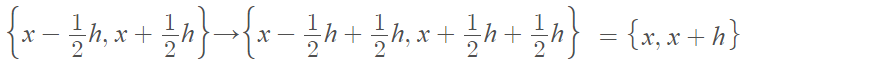
Sliding in this way doesn’t preserve differentiability but it does preserve the property of being a derivative [4].
References
[1] Sinclair, T. (2016). MA 34100 Fall 2016, HW 9. Retrieved August 9, 2021 from: https://www.math.purdue.edu/~tsincla/341-f16/hw-9.pdf
[2] Washburn, L. The Lanczos Derivative.
[3] The Math Doctors. The Symmetric Derivative. Retrieved August 9, 2021 from: https://www.themathdoctors.org/the-symmetric-derivative/
[4] Ash, J. Topics in Generalized Differentiation. Retrieved August 9, 2021 from:https://math.depaul.edu/~mash/Seville.pdf