What is Integration by Parts?
Integration by parts is used to integrate when you have a product (multiplication) of two functions. For example, you would use integration by parts for ∫x · ln(x) or ∫ xe5x.
In a way, it’s very similar to the product rule, which allowed you to find the derivative for two multiplied functions. With the product rule, you labeled one function “f”, the other “g”, and then you plugged those into the formula. However, while the product rule was a “plug and solve” formula (f′ * g + f * g), the integration equivalent of the product rule requires you to make an educated guess about which function part to put where.
Formula
The formula for integration by parts is:
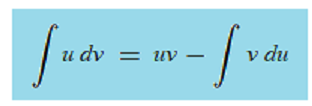
The left part of the formula gives you the labels (u and dv).
Using the Formula
General steps to using the integration by parts formula:
- Choose which part of the formula is going to be u. Ideally, your choice for the “u” function should be the one that’s easier to find the derivative for. For example, “x” is always a good choice because the derivative is “1”.
- Label the remaining function “dv“.
- Solve the formula.
The idea is fairly simple—you split the formula into two parts to make solving it easier; The hard part is deciding which function to name f, and which to name g. Notice that the formula only requires one derivative (f’), but it also has an integral (∫). If you choose the wrong part for “f”, you might end up with a function that’s more complicated to integrate than the one you start with. That will probably happen often at first, until you get to recognize which functions transform into something that’s easily integrated. If you end up with a problematic function, it’s an easy fix: go back a couple of steps and swap your choices over.
Example
Example Problem: Integrate
f(x) = x e-x dx
Step 1: Choose “u”. As noted above in the general steps, you want to pick the function where the derivative is easier to find. The derivative of “x” is just 1, while the derivative of e-x is e-x (which isn’t any easier to solve). So here, we’ll pick “x” for the “u”. Substituting, we get:
u = x
Step 2: Find “du” by taking the derivative of the “u” you chose in Step 1. Make sure you also write the “dx” after the derivative:
du = 1 dx
du = dx
Set this part aside for a moment.
Step 3: Choose “dv”. This is the part that’s left over from step 1.
dv = e-x
Step 4: Integrate Step 3 to find “v”: The integral of e-x is -e-x (using u-substitution).
v = -e-x
Step 5: Use the information from Steps 1 to 4 to fill in the formula. To recap:
u = x (Step 1)
v = -e-x (Step 4)
du = dx
dv = e-x
Plugging those values into the right hand side of the formula
uv – ∫v du:
x (-e-x) – ∫ -e-x dx
Tidying up those negatives:
-xe-x + ∫e-x
That’s it!
Next: An alternative method: Tabular Integration.