Contents (click to skip to that section):
Topological Space Definition

A topological space is a set X with well defined, open subsets T which have four special properties:
- The empty set (a set containing no elements) is in T
- X, the original set, is in T
- The intersection of a finite number of sets T is also in T
- The union of an arbitrary number of sets in T is also in T
A structure of subsets satisfying the above properties is called a topology, so we can say that a set X taken together with its topology is a topological space.
It’s important to realize that a set X may be the basis for more than topological space, since each topological space is considered the set taken together with its topology, if it has a different topology it is a different topology space.
If we have X and a set of closed subsets, we can write a slightly different but analogous definition.
Topological Space in Terms of Neighborhoods
Another way of thinking about a topological space is as a set of points along with the set of neighborhoods of each point. There are some axioms relating sets, points, and their neighborhoods which this construction must follow. These are listed below
- Every point belongs to every one of its neighborhoods; if N is a neighborhood of x, x belongs to N.
- Suppose N is a subset of X, and suppose that N includes a neighborhood of x in X. Then N is a neighborhood of x.
- If I is an intersection of two neighborhoods of x, I is a neighborhood of X.
- Every neighborhood N of x also includes a neighborhood M of x, and N is a neighborhood of each point of M
.
A function space is just a space made of functions; It’s one set of functions that maps to another set of functions.
As a simple example, let’s say you have fn:ℝ → ℝ, with fn(x) = xn, n = 0, 1, 2. The set {f0, f1, f2} is a function space. A more complex example is L2[a, b], the set of real-valued functions square integrable on the closed interval [a, b].
Notations include X→Y or YX.
Types of Function Space
All function spaces map one set of functions to another. In a basic sense, topological spaces and vector spaces are types of functions spaces. However, whenever we refer to function spaces, or function space theory, we’re usually talking about a wide variety of spaces that vary from the simple to the more complex, to the point that they may become very abstract (especially in high dimensional spaces).
Usually (but not always), function spaces are associated with a norm which fully describes the extent of the function space (e.g. direction, orientation etc.).
Some common function spaces include:
- C [a, b] Continuous functions on [a, b] with norm
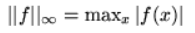
- L1(a, b) Integrable functions ∫ |f(x)|2 dx < +∞ with norm

- L2(a, b)Square integrable functions ∫ |f(x)|p dx < +∞ where (p ≥ 1) with norm

Use of Spaces
![]() spaces are useful in the study of ordinary and partial differential equations. Although many of these spaces have shortcomings when applied to partial differential equations, more sophisticated and modern spaces include Hölder spaces and Sobolev spaces .
spaces are useful in the study of ordinary and partial differential equations. Although many of these spaces have shortcomings when applied to partial differential equations, more sophisticated and modern spaces include Hölder spaces and Sobolev spaces .
Many other different types of function spaces appear in classical and modern mathematics, including Bessel-potential spaces, Besov spaces, and Lebesgue spaces.
Topological Space Definition / Function SpaceReferences
MIT. Math Camp 1: Functional analysis. Retrieved February 19, 2020 from: https://www.mit.edu/~9.520/spring09/
Stewart, D. (1998). Function Spaces. Retrieved February 19, 2020 from: http://homepage.cs.uiowa.edu/~dstewart/classes/22m176/dfs-notes/node2.html
Tang, C. & Zhai, Z. (2010). Generalized Poincaré embeddings and weighted Hardy operator on Q α,q/p spaces. J. Math. Anal. Appl. 371 665–676
Triebel, H. (2010). Theory of Function Spaces. Birkhäuser.
Vokrinek, Lukas. Essential Topology. Retrieved from http://www.math.muni.cz/~koren/EssentialTopology.pdf on January 20, 2019