Calculus Problem Solving > Related Rates
Related rate problems involve functions where a relationship exists between two or more derivatives. For example, you might want to find out the rate that the distance is increasing between two airplanes.
Solving related rate problems has many real life applications. For example, a gas tank company might want to know the rate at which a tank is filling up, or an environmentalist might be concerned with the rate at which a certain marshland is flooding.
Solving the problems usually involves knowledge of geometry and algebra in addition to calculus. Often, the “hard” part is the geometry or algebra—not the calculus, so you’ll want to make sure you brush up on those skills. Solving related relate problems also involves applications of the chain rule and implicit differentiation—where you differentiate both sides of the equation.
Example problems:
- Ripples in a pond
- Length and width of a draining pond
- Speed of an airplane
- Changing angle of elevation
Related Rates Example problem #1
Q. A rock is dropped into the center of a circular pond. The ripple moved outward at 4 m/s. How fast does the area change, with respect to time, when the ripple is 3m from the center?
Step 1: Draw a picture of the problem (this always helps, especially when geometry is involved).
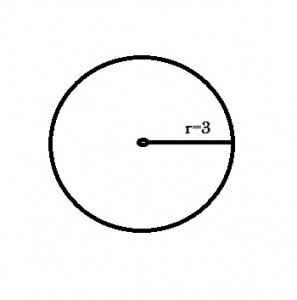
Step 2: Write out what you know about the problem, using equations. You know that the rate at which the ripple (r, the radius of the circle) is moving, with respect to time t, is 4 m/s, so:
- dr/dt = 4 m/s
Step 3: Write out what you want to know (what you are trying to solve for). You want to know how fast the area A is changing with respect to time t:
- dA/dt = x, when r = 3m
Step 4: Use the chain rule to find a solution for your Step 3 equation. The chain rule tells us that:
- dA/dt = dA/dr * dr/dt
Step 5: Figure out what dA/dr is. From geometry, we know that A = πr2. So dA/dr is just the derivative of A = πr2.
- d/dr[A] = d/dr[πr2]
- = dA/dr = 2πr
- So: dA/dt = 2πr * dr/dt
Step 6: Solve the Step 5 equation. You know that dr/dt (from Step 2) is 4 m/s, and r is 3 m (from the question), so:
- dA/dt = 2π(3) * 4 m/s
- = 24π m2/s
That’s it!

Related Rates Example problem #2:
The length of a rectangular drainage pond is changing at a rate of 8 ft/hr and the perimeter of the pond is changing at a rate of 24 ft/hr. At what rate is the width changing?
Step 1: Figure out which geometric formulas are related to the problem. From basic geometry, the formula for perimeter is P = (2*l) + (2*w) and that A = l*w.
Step 2: Differentiate the perimeter equation:
dp/dt = (2*dl/dt) + (2*dw/dt)
Step 3: Substitute in the information you know from the question. You know that the rate at which the perimeter is changing is 24 ft/hr and the length is changing at 8 ft/hr, so (using algebra):
- 24 = (2*8) + (2*dw/dt)
- Dividing by 2 gives us: 12 = 8 + dw/dt
- Subtracting 8 from both sides: 4 = dw/dt
The width of the drainage pond is changing at 4 ft/hr.
That’s it!
Related Rates Example #3: Speed of an Airplane
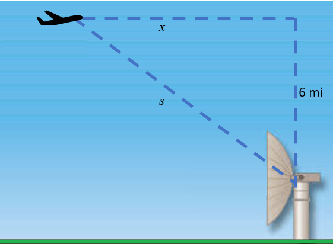
An airplane is flying towards a radar dish. Its distance from the dish (s) decreases at a rate of 400 miles per hour when s = 10 miles. How fast is the plane going?
Solution:
Step 1: Find x using the Pythagorean theorem, using the information in the question that s = 10 and the height is 6:
x = √(102 – 62) = 8
Step 2: State the given rate: (ds/dt) = -400
Step 3: Set up the Pythagorean theorem again, this time with x as the horizontal distance from the radar. You are given the height (y) in the question (6):
x2 + 62 = s2
Step 4: Differentiate. I used the power rule and the fact that the derivative of a constant is zero to get:
2x (dx/dt) = 2s (ds/dt)
which simplifies to
x (dx/dt) = s (ds/dt) & rarr; (dx/dt) = s/x (ds/dt)
Step 5:Substitute for s, x and (ds/dt). From the question, s = 10 miles and we have x = 8 from Step 1 and ds/dt = -400 from Step 2:
=10/8 = -400
The velocity is -400, so the speed (without the directional negative sign) is 500 miles per hour.
Related Rates Example #4: Changing Angle of Elevation
A TV station is filming 2000 feet from the take off of a rocket. What is the rate of change in the angle of elevation 10 seconds after lift off, given that the position function of the rocket is s = 50t2?
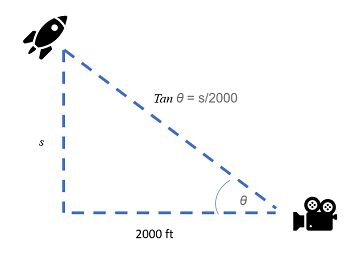
Step 1: Solve the position function for the height (at 10 seconds):
- s = 50t2 = 50(10)2 = 5000 feet.
Step 2: Differentiate the position function to get the velocity function (in ft. per second):
- V(t) = 100t
Step 3: (Here’s where your trigonometry knowledge comes in: remember SOHCAHTOA?): Differentiate Tan θ = s / 2000 with respect to t:
Tan θ = s / 2000
(sec2θ) (dθ/dt) = 1/2000 (ds/dt)
Step 4: Substitute the rate (from Step 2) in for (ds/dt):
dθ/dt = cos2θ 100t/2000
Step 5: From trigonometry, we know that Step 4 can be rewritten (substituting cosθ = 2000/√(s2 + 20002):
dθ/dt = (2000/√(s2 + 20002)) 100t/2000.
Step 6: Solve, using t = 10 (from the question) and s = 5000 (Step 1):
dθ/dt = (2000(100)(10))/(50002 + 20002) = 2/29
10 seconds after lift off, the angle of elevation changes at a rate of 2/29 radians per second.
References
Larson, R. & Edwards, B. (2018). Calculus: Early Transcendentals. Cengage Learning.