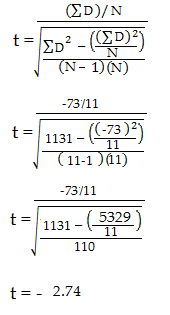T Test (Student’s T-Test): Definition and Examples

T Test: Contents:

• What is a T Test?
• The T Score
• T Values and P Values
• Calculating the T Test
• What is a Paired T Test (Paired Samples T Test)?

What is a T test?

Watch the video for an overview of the T-test:

The t test tells you how significant the differences between group means are. It lets you know if those differences in means could have happened by chance. The t test is usually used when data sets follow a normal distribution but you don’t know the population variance.

For example, you might flip a coin 1,000 times and find the number of heads follows a normal distribution for all trials. So you can calculate the sample variance from this data, but the population variance is unknown. Or, a drug company may want to test a new cancer drug to find out if it improves life expectancy. In an experiment, there’s always a control group (a group who are given a placebo, or “sugar pill”). So while the control group may show an average life expectancy of +5 years, the group taking the new drug might have a life expectancy of +6 years. It would seem that the drug might work. But it could be due to a fluke. To test this, researchers would use a Student’s t-test to find out if the results are repeatable for an entire population.

In addition, a t test uses a t-statistic and compares this to t-distribution values to determine if the results are statistically significant.

However, note that you can only uses a t test to compare two means. If you want to compare three or more means, use an ANOVA instead.

The T Score.

The t score is a ratio between the difference between two groups and the difference within the groups.

• Larger t scores = more difference between groups.
• Smaller t score = more similarity between groups.

A t score of 3 tells you that the groups are three times as different from each other as they are within each other. So when you run a t test, bigger t-values equal a greater probability that the results are repeatable.

T-Values and P-values

How big is “big enough”? Every t-value has a p-value to go with it. A p-value from a t test is the probability that the results from your sample data occurred by chance. P-values are from 0% to 100% and are usually written as a decimal (for example, a p value of 5% is 0.05). Low p-values indicate your data did not occur by chance. For example, a p-value of .01 means there is only a 1% probability that the results from an experiment happened by chance.

Calculating the Statistic / Test Types

There are three main types of t-test:

• An Independent Samples t-test compares the means for two groups.
• A Paired sample t-test compares means from the same group at different times (say, one year apart).
• A One sample t-test tests the mean of a single group against a known mean.

You can find the steps for an independent samples t test here. But you probably don’t want to calculate the test by hand (the math can get very messy. Use the following tools to calculate the t test:

• How to do a T test in Excel.
• T test in SPSS.
• T-distribution on the TI 89.
• T distribution on the TI 83.

What is a Paired T Test (Paired Samples T Test / Dependent Samples T Test)?

A paired t test (also called a correlated pairs t-test, a paired samples t test or dependent samples t test) is where you run a t test on dependent samples. Dependent samples are essentially connected — they are tests on the same person or thing. For example:

• Knee MRI costs at two different hospitals,
• Two tests on the same person before and after training,
• Two blood pressure measurements on the same person using different equipment.

When to Choose a Paired T Test / Paired Samples T Test / Dependent Samples T Test

Choose the paired t-test if you have two measurements on the same item, person or thing. But you should also choose this test if you have two items that are being measured with a unique condition. For example, you might be measuring car safety performance in vehicle research and testing and subject the cars to a series of crash tests. Although the manufacturers are different, you might be subjecting them to the same conditions.

With a “regular” two sample t test, you’re comparing the means for two different samples. For example, you might test two different groups of customer service associates on a business-related test or testing students from two universities on their English skills. But if you take a random sample each group separately and they have different conditions, your samples are independent and you should run an independent samples t test (also called between-samples and unpaired-samples).

The null hypothesis for the independent samples t-test is μ₁ = μ₂. So it assumes the means are equal. With the paired t test, the null hypothesis is that the pairwise difference between the two tests is equal (H₀: µ_d = 0).

Paired Samples T Test By hand

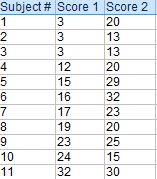
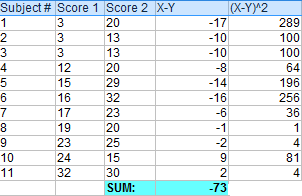
Example question: Calculate a paired t test by hand for the following data:

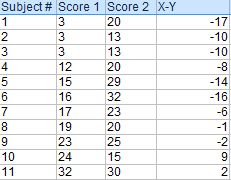
Step 1: Subtract each Y score from each X score.

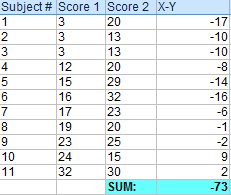
Step 2: Add up all of the values from Step 1 then set this number aside for a moment.

Step 3: Square the differences from Step 1.

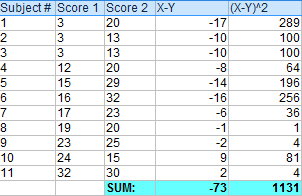
Step 4: Add up all of the squared differences from Step 3.

Step 5: Use the following formula to calculate the t-score:

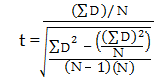
1. The “ΣD” is the sum of X-Y from Step 2.
2. ΣD²: Sum of the squared differences (from Step 4).
3. (ΣD)²: Sum of the differences (from Step 2), squared.

If you’re unfamiliar with the Σ notation used in the t test, it basically means to “add everything up”. You may find this article useful: summation notation.

Step 6: Subtract 1 from the sample size to get the degrees of freedom. We have 11 items. So 11 – 1 = 10.

Step 7: Find the p-value in the t-table, using the degrees of freedom in Step 6. But if you don’t have a specified alpha level, use 0.05 (5%).

So for this example t test problem, with df = 10, the t-value is 2.228.

Step 8: In conclusion, compare your t-table value from Step 7 (2.228) to your calculated t-value (-2.74). The calculated t-value is greater than the table value at an alpha level of .05. In addition, note that the p-value is less than the alpha level: p <.05. So we can reject the null hypothesis that there is no difference between means.

However, note that you can ignore the minus sign when comparing the two t-values as ± indicates the direction; the p-value remains the same for both directions.

In addition, check out our YouTube channel for more stats help and tips!

References

Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, pp. 50-55, 1956.

---------------------------------------------------------------------------

Need help with a homework or test question? With Chegg Study, you can get step-by-step solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is free!

Comments? Need to post a correction? Please Contact Us.