Contents:
What does it mean to reject the null hypothesis?
Watch the video for an example:
In many statistical tests, you’ll want to either reject or support the null hypothesis. For elementary statistics students, the term can be a tricky term to grasp, partly because the name “null hypothesis” doesn’t make it clear about what the null hypothesis actually is!
Overview
The null hypothesis can be thought of as a nullifiable hypothesis. That means you can nullify it, or reject it. What happens if you reject the null hypothesis? It gets replaced with the alternate hypothesis, which is what you think might actually be true about a situation. For example, let’s say you think that a certain drug might be responsible for a spate of recent heart attacks. The drug company thinks the drug is safe. The null hypothesis is always the accepted hypothesis; in this example, the drug is on the market, people are using it, and it’s generally accepted to be safe. Therefore, the null hypothesis is that the drug is safe. The alternate hypothesis — the one you want to replace the null hypothesis, is that the drug isn’t safe. Rejecting the null hypothesis in this case means that you will have to prove that the drug is not safe.

Vioxx was pulled from the market after it was linked to heart problems.
To reject the null hypothesis, perform the following steps:
Step 1: State the null hypothesis. When you state the null hypothesis, you also have to state the alternate hypothesis. Sometimes it is easier to state the alternate hypothesis first, because that’s the researcher’s thoughts about the experiment. How to state the null hypothesis (opens in a new window).
Step 2: Support or reject the null hypothesis. Several methods exist, depending on what kind of sample data you have. For example, you can use the P-value method. For a rundown on all methods, see: Support or reject the null hypothesis.
If you are able to reject the null hypothesis in Step 2, you can replace it with the alternate hypothesis.
That’s it!
When to Reject the Null hypothesis
Basically, you reject the null hypothesis when your test value falls into the rejection region. There are four main ways you’ll compute test values and either support or reject your null hypothesis. Which method you choose depends mainly on if you have a proportion or a p-value.
Support or Reject the Null Hypothesis: Steps
Click the link the skip to the situation you need to support or reject null hypothesis for:
General Situations: P Value
P Value Guidelines
A Proportion
A Proportion (second example)
Support or Reject Null Hypothesis with a P Value
If you have a P-value, or are asked to find a p-value, follow these instructions to support or reject the null hypothesis. This method works if you are given an alpha level and if you are not given an alpha level. If you are given a confidence level, just subtract from 1 to get the alpha level. See: How to calculate an alpha level.
Step 1: State the null hypothesis and the alternate hypothesis (“the claim”).
If you aren’t sure how to do this, follow this link for How To State the Null and Alternate Hypothesis.
Step 2: Find the critical value. We’re dealing with a normally distributed population, so the critical value is a z-score.
Use the following formula to find the z-score.
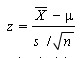
Click here if you want easy, step-by-step instructions for solving this formula.
Step 4: Find the P-Value by looking up your answer from step 3 in the z-table. To get the p-value, subtract the area from 1. For example, if your area is .990 then your p-value is 1-.9950 = 0.005. Note: for a two-tailed test, you’ll need to halve this amount to get the p-value in one tail.
Step 5: Compare your answer from step 4 with the α value given in the question. Should you support or reject the null hypothesis?
If step 7 is less than or equal to α, reject the null hypothesis, otherwise do not reject it.
P-Value Guidelines
Use these general guidelines to decide if you should reject or keep the null:
If p value > .10 → “not significant”
If p value ≤ .10 → “marginally significant”
If p value ≤ .05 → “significant”
If p value ≤ .01 → “highly significant.”
That’s it!
Support or Reject Null Hypothesis for a Proportion
Sometimes, you’ll be given a proportion of the population or a percentage and asked to support or reject null hypothesis. In this case you can’t compute a test value by calculating a z-score (you need actual numbers for that), so we use a slightly different technique.
Watch the video for an example:
Example question: A researcher claims that Democrats will win the next election. 4300 voters were polled; 2200 said they would vote Democrat. Decide if you should support or reject null hypothesis. Is there enough evidence at α=0.05 to support this claim?
Step 1: State the null hypothesis and the alternate hypothesis (“the claim”).
Ho:p ≤ 0.5
H1:p > .5
Step 2: Compute ![]() by dividing the number of positive respondents from the number in the random sample:
by dividing the number of positive respondents from the number in the random sample:
2200/4300 = 0.512.
Step 3: Use the following formula to calculate your test value.
![]()
Where:
Phat is calculated in Step 2
P the null hypothesis p value (.05)
Q is 1 – p
The z-score is:
.512 – .5 / √(.5(.5) / 4300)) = 1.57
Step 4: Look up Step 3 in the z-table to get .9418.
Step 5: Calculate your p-value by subtracting Step 4 from 1.
1-.9418 = .0582
Step 6: Compare your answer from step 5 with the α value given in the question. Support or reject the null hypothesis? If step 5 is less than α, reject the null hypothesis, otherwise do not reject it. In this case, .582 (5.82%) is not less than our α, so we do not reject the null hypothesis.
Support or Reject Null Hypothesis for a Proportion: Second example
Example question: A researcher claims that more than 23% of community members go to church regularly. In a recent survey, 126 out of 420 people stated they went to church regularly. Is there enough evidence at α = 0.05 to support this claim? Use the P-Value method to support or reject null hypothesis.
Step 1: State the null hypothesis and the alternate hypothesis (“the claim”). Ho:p ≤ 0.23; H1:p > 0.23 (claim)
Step 2: Compute ![]() by dividing the number of positive respondents from the number in the random sample:
by dividing the number of positive respondents from the number in the random sample:
63 / 210 = 0.3.
Step 3: Find ‘p’ by converting the stated claim to a decimal:
23% = 0.23.
Also, find ‘q’ by subtracting ‘p’ from 1: 1 – 0.23 = 0.77.
Step 4: Use the following formula to calculate your test value.
![]()
Click here if you want easy, step-by-step instructions for solving this formula.
If formulas confuse you, this is asking you to:
- Subtract p from
 (0.3 – 0.23 = 0.07). Set this number aside.
(0.3 – 0.23 = 0.07). Set this number aside. - Multiply p and q together, then divide by the number in the random sample. (0.23 x 0.77) / 420 = 0.00042
- Take the square root of your answer to 2. √(0.1771) = 0.0205
- Divide your answer to 1. by your answer in 3. 0.07 / 0.0205 = 3.41
Step 5: Find the P-Value by looking up your answer from step 5 in the z-table. The z-score for 3.41 is .4997. Subtract from 0.500: 0.500-.4997 = 0.003.
Step 6: Compare your P-value to α. Support or reject null hypothesis? If the P-value is less, reject the null hypothesis. If the P-value is more, keep the null hypothesis.
0.003 < 0.05, so we have enough evidence to reject the null hypothesis and accept the claim.
Note: In Step 5, I’m using the z-table on this site to solve this problem. Most textbooks have the right of z-table. If you’re seeing .9997 as an answer in your textbook table, then your textbook has a “whole z” table, in which case don’t subtract from .5, subtract from 1. 1-.9997 = 0.003.
Check out our Youtube channel for video tips!
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.