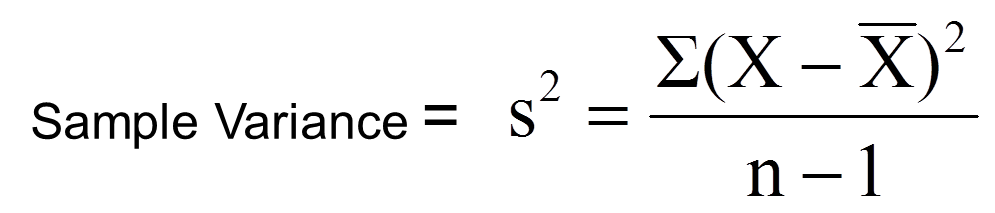
What is a Point Estimate?
In simple terms, any statistic can be a point estimate. A statistic is an estimator of some parameter in a population. For example:
- The sample standard deviation (s) is a point estimate of the population standard deviation (σ).
- The sample mean (̄x) is a point estimate of the population mean, μ.
- The sample variance (s2) is a point estimate of the population variance (σ2).
In more formal terms, the estimate occurs as a result of point estimation applied to a set of sample data. Points are single values, in comparison to interval estimates, which are a range of values. For example, a confidence interval is one example of an interval estimate.
Finding the Estimates
Four of the most common ways to find an estimate:
- The Method of Moments: is based on the law of large numbers and uses relatively simple equations to find point estimates. Is often not too accurate and has a tendency to be biased. More info.
- Maximum Likelihood: uses a model (for example, the normal distribution) and uses the values in the model to maximize a likelihood function. This results in the most likely parameter for the inputs selected.
- Bayes Estimators: minimize the average risk (an expectation of random variables). More info.
- Best Unbiased Estimators: several unbiased estimators can be used to approximate a parameter. Which one is “best” depends on what parameter you are trying to find. For example, with variance, the estimator with the smallest variance is “best”. More info.
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
“Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.”