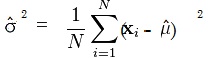Statistics Definitions > Method of Moments
You may want to read this article first: What are moments?.
What is Method of Moments?
The method of moments is a way to estimate population parameters, like the population mean or the population standard deviation. The basic idea is that you take known facts about the population, and extend those ideas to a sample. For example, it’s a fact that within a population:
Expected value E(x) = μ
For a sample, the estimator
![]()
is just the sample mean, x̄ . The formula for the sample mean is:
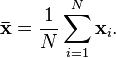
This is the first moment condition.
The second moment condition involves the variance. The population variance is Var(x) = σ2, so we just need to use the method of moments to estimate the variance in the sample. Here’s how the formula is derived:
- Use the fact that the population variance Var(x) = σ2 is the same as: E(x – μ)2 = σ2.
- As in the first moment, replace the population expectation by the sample equivalent (the sample mean). However, while the first moment was the sample mean of x, this time it’s x – μ, giving the formula:

The same principal is used to derive higher moments like skewness and kurtosis:
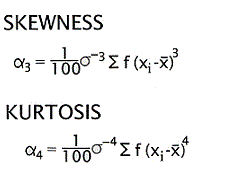
The above method is probably the most widely used method of moments. There is another method, which uses sample moments about the mean instead of sample moments about the origin.
Advantages and Disadvantages
Advantages
- Method of moments is simple (compared to other methods like the maximum likelihood method) and can be performed by hand.
Disadvantages
- The parameter estimates may be inaccurate. This is more frequent with smaller samples and less common with large samples.
- The method may not result in sufficient statistics. In other words, it may not take into account all of the relevant information in the sample.