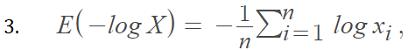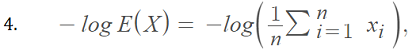Statistics Definitions > Arithmetic Mean
Contents:
- What is the Arithmetic Mean?
- How to find it (Examples)
- Population vs. Sample Mean
- Showing the Arithmetic Mean is Greater than the Geometric Mean
What is the Arithmetic Mean?
The arithmetic mean is another name for the mean or the average. When someone talks about the mean of a data set, they are usually talking about the arithmetic mean (most people just drop the word “arithmetic”). It’s called a different name to set it apart from other means found in math, including the geometric mean.
The mean is influenced by outliers , so it isn’t always a good indicator of where the middle of a data set is. For data sets that have either a lot of low values or a lot of high values, the median is often a better way to describe the “middle.”
How to find the Arithmetic Mean
Finding the arithmetic mean takes two steps: add all the numbers up and then divide by the number of items in your set. The arithmetic mean is found in the exact same way as a sample mean (“sample” here just means a number of items in your data set). Watch the video, or read the steps below:
Example problem: Find the arithmetic mean for average driving speed for one car over a 6 hour journey: 54 mph, 57 mph, 58 mph, 66 mph, 69 mph, 71 mph
Step 1: Add all the numbers up: 54 + 57 + 58 + 66 + 69 + 71 = 375.
Step 2: Divide by the number of items in the set. For this set there are 6 numbers, so:
375 / 6 = 62.5.
Solution: The average driving speed is 62.5 mph.
For another example with steps, see the next article:
How to find the mean
Population vs. Sample Mean
If your data is a population, then the mean is called a population mean, represented by the letter μ. If the list is a sample, it’s called a sample mean x̄.
Showing the Arithmetic Mean is Greater than the Geometric Mean
Jensen’s inequality, usually taught in a calculus based statistics course, can be used to show that the arithmetic mean of n positive scalars x1,x2,…xn, is greater than or equal to their geometric mean, which is equal to
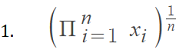
Where Π is product notation.
This statement can be shown by considering a convex function f(x) = -log x. Let X be a discrete random variable with values x1,x2,…xn, and probabilities 1/n [1]:
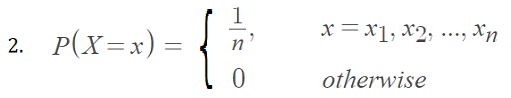
By Jensen’s inequality:
E (-log X) ≥ –log E(X).
However:
and
With 3. & 4. in Jensen’s inequality, we have:
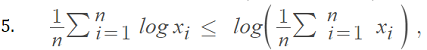
or
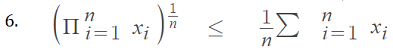
The logarithm function is monotone increasing, so we can conclude that:
Check out our YouTube channel for hundreds of statistics and calculus videos.
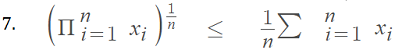
References
[1] Khuri, A. Advanced Calculus with Applications in Statistics. Second Edition. Wiley.