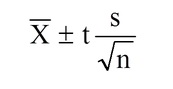Statistics Definitions > Interval Estimate
What is an Interval Estimate?
An interval is a range of values for a statistic. For example, you might think that the mean of a data set falls somewhere between 10 and 100 (10 < μ < 100). A related term is a point estimate, which is an exact value, like μ = 55.
As an example, let’s say you wanted to find out the average cigarette use of senior citizens. You can’t survey every senior citizen on the planet (due to time constraints and finances), so you take a sample of 1000 senior citizens and find that 10% of them smoke cigarettes. Although you’ve only taken a sample, you can use that figure to estimate that “about” 10% of the whole population smoke cigarettes. In reality, it’s unlikely to be exactly 10% (as you only sampled a small percentage of people), but it’s probably somewhere around there, perhaps between 5 and 15%. That “somewhere between 5 and 15%” is an interval estimate.
Confidence Levels and Interval Estimates
There’s nothing wrong with making a good guess at an interval, but sometimes we want to be very confident that our results are sound and repeatable. “Repeatable” means that if you do the whole thing over again, you’ll get the same results. One way to do this is to express a confidence level. Confidence levels are percentages of certainty. For example, you might say you are 99% confident (i.e. you have a 99% confidence level) that between 5 and 15% of senior citizens smoke cigarettes. When the interval estimate has a confidence level attached, it’s called a confidence interval. The lower bound (in this example, 5%) is called a lower confidence limit and the upper bound (in this example, 15%) is called an upper confidence limit.
But how confident are you that the range is from 5 to 15%? Are you 99% sure? 90% sure? Less? How you figure this is out is with probability theory: you want to find out the possibility that your results could be due to chance alone (as opposed to your results being repeatable).