Standard Form: Simple Definition, Examples

Calculus Definitions >

The standard form of any line in a Cartesian plane is Ax + By = C where:

• A, B, and C are placeholders for constants (at least one of A and B must be nonzero),
• x and y are variables.

This form differs from the “usual” slope-intercept form you come across in calculus: y = mx + b or the point-slope form (which is really just a rearrangement of slope-intercept): y – y₁ = m (x – x₁).

As a quick check of your understanding, which two of the following equations are in standard form?


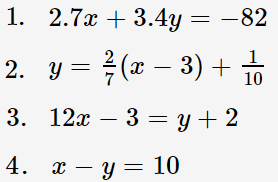
See the solution here.

Example of Rewriting in Standard Form

Example Question: Rewrite y = 3x – 4 in standard form.

Step 1: Flip the equation (this gets the Ax term in the right place):
3x – 4 = y

Step 2: Subtract “y” from both sides:
3x – y – 4 = 0

Step 3: Add 4 to both sides:
3x – y = 4

That’s it!

Why Do We Need Standard Form?

Sometimes, it’s easier to work with equations that are in a standard form. For example, it’s easier to identify the center of a circle (h, k) and the radius (r) if the equation is in standard form: (x – h)² + (y – k)² = r². Compare that to the general form x² + y² + Dx + Ey + F = 0, where D, E, F are constants.

On the other hand, the slope and y-intercept of a line are easier to see in slope-intercept form, so that’s it’s handy to be able to switch between the different forms.

In calculus, you’ll mostly be working with the standard generalized form of the linear equation (Ax + Bx + C). However, you’ll occasionally need some others. They include:
For a parabola, the standard form is either:

• (x – h)² = a (y – k), or
• (y – k)² = a(x – h).

Ellipsoid:

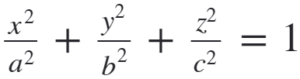
Two of the equations in the example above are in standard form: 1 and 4:

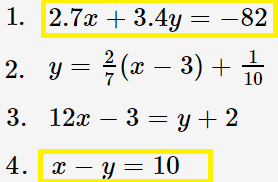
Related articles:

• Trinomial in standard form.
• Polynomial in Standard Form

References

Lazari, A. (2020). Equation of a Circle. Retrieved October 20, 2020 from: https://mypages.valdosta.edu/alazari/math1111/Circle.html