Einstein Summation, introduced by Einstein in 1916 in his generalized theory of relativity paper, is a shorthand way to avoid the tedium of writing summations. It is stated as:
“If a suffix occurs twice in a term, once in the lower position and once in the upper position, that suffix implies sum over a defined range.”
This convention tells us that expressions with a repeated index (one raised and one lowered) can have the sign of summation omitted; Instead, you can implicitly sum over that index from 1 to n (Weinstein, 2016). If the range isn’t specified, you can assume it is from 1 to n (Islam, 2006).
The Einstein summation convention is used frequently in physics. For example, index notation is useful for keeping track of vector components v = (v1, v2, v3). It is common in physics for Greek indices (used for space and time components), but not necessarily Latin indices (used for spatial components) (Helrich, 2016).
Examples of Einstein Summation
A very simple example of Einstein summation is the following definition of a dot product:
A•B = Ai Bi
A slightly more complex example involves a series:
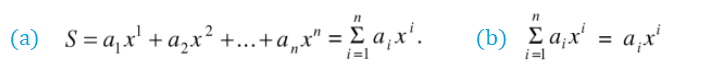
A repeated index (usually i) means to sum over that index.
Einstein Summation Rules
Einstein summation only applies to very specific summations which follow four basic rules (Evans, 2020):
- The summation sign is omitted.
- A summation is implied if the index appears twice. For example, AiBi = A1sub>B1 + A2B2 + A3B3, where i is a dummy index. It’s called a “dummy index” as you can use anything here (i, j, k,…) and it doesn’t change the summation.
- A suffix appearing just once can take any value. For example, Ai = Bi holds for i = 1, 2, 3. (there can be multiple free indices i).
Note that there may be more than one free index and they must be the same on both sides of an equation. For example, Gi = Hj is wrong. - A suffix can’t appear more than two times.
References
Evans, M. (2020). Lecture 5: More About Suffix Notation. Retrieved November 18, 2020 from: https://www2.ph.ed.ac.uk/~mevans/mp2h/VTF/lecture05.pdf
Helrich, C. (2016). Analytical Mechanics. Springer.
Weinstein, G. (2016). General Relativity Conflict and Rivalries: Einstein’s Polemics with Physicists. Cambridge Scholar Publishing.
Islam, N. (2006). Tensor Algebra. New Age International.