Contents:
What is an Initial Condition?
Differential Equation Initial Value Problem Example.
What is an Initial Condition?
An initial condition is a starting point; Specifically, it gives dependent variable values (or one of its derivatives) for a certain independent variable. It allows you to zoom in on a specific solution.
In general, an initial condition can be any starting point. For example, you might want to define an initial pressure or a starting balance in a bank account. In statistics, it’s a nuisance parameter in unit root testing (Muller & Elliot, 2003). In calculus, the term usually refers to the starting condition for finding the particular solution for a differential equation.
Initial Condition at a Discontinuity
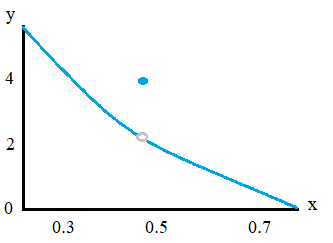
Use in Differential Equations
The “initial” condition in a differential equation is usually what is happening when the initial time (t) is at zero (Larson & Edwards, 2008). For example, let’s say you have some function g(t), you might be given the following initial condition:
- g(0) = 40 (the function returns a value of 40 at t = 0 seconds)
- g′(0) = 32 (the value of the first derivative at t = 0 seconds is 32)
An initial condition leads to a particular solution; If you don’t have an initial value, you’ll get a general solution.
Differential Equation Initial Value Problem.
Watch the video for two examples:
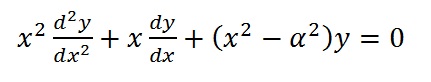
For example, the differential equation needs a general solution of a function or series of functions (a general solution has a constant “c” at the end of the equation):
dy⁄dx = 19x2 + 10
But if an initial condition is specified, then you must find a particular solution (a single function). For example:
dy⁄dx19x2 + 10; y(10) = 5.
Finding a particular solution for a differential equation requires one more step—simple substitution—after you’ve found the general solution.
Initial Value Problem: Examples
Example Problem 1: Solve the following differential equation, with the initial condition y(0) = 2.
dy⁄dx = 10 – x
Step 1: Use algebra to move the “dx” to the right side of the equation (this makes the equation more familiar to integrate):
dy⁄dx = 10 – x →
dy = 10 – x dx
Step 2: Integrate both sides of the equation.
- ∫dy = ∫10 – x dx →
- ∫1 dy = ∫10 – x dx →
- y = 10x – x2⁄2 + C
Step 3: Substitute in the values specified in the initial condition. In this sample problem, the initial condition is that when x is 0, y=2, so:
- 2 = 10(0) – 02⁄2 + C
- 2 = 0 + C
- C = 2
Therefore, the function that satisfies this particular differential equation with the initial condition y(0) = 2 is y = 10x – x2⁄2 + 2
That’s it!
Initial Value Example problem #2: Solve the following initial value problem: dy⁄dx = 9x2 – 4x + 5; y(-1) = 0
Step 1: Rewrite the equation, using algebra, to make integration possible (essentially you’re just moving the “dx”.
- dy⁄dx = 9x2 – 4x + 5 →
- dy = (9x2 – 4x + 5) dx
Step 2: Integrate both sides of the differential equation to find the general solution:
- ∫ dy = ∫(9x2 – 4x + 5) dx →
- ∫ 1 dy = ∫(9x2 -4x + 5) dx →
- y = (9x3⁄3 – 4x2⁄2 + 5x + C →
- y=3x3-2x2 + 5x + C
Step 3: Evaluate the equation you found in Step 3 for when x = -1 and y = 0.
0 = 3(-1)3 -2(-1)2 + 5(-1) + C →
0 = -3 -2 – 5 + C →
0 = -10 + C
c = 0
Therefore, the particular solution to the initial value problem is y = 3x3 – 2x2 + 5x + 10
That’s it!
References
Larson, R. & Edwards, B. (2008). Calculus of a Single Variable. Cengage Learning.
MIT Open Courseware. Initial Conditions. Retrieved July 19, 2020 from: https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-iii-fourier-series-and-laplace-transform/unit-step-and-unit-impulse-response/MIT18_03SCF11_s25_1text.pdf
Muller, U. & Elliot, G. (2003). Tests for Unit Roots. Econometrica, Vol. 71, No. 4 (July), 1269–1286
Calculus.