Calculus Problem Solving > Surface Area Calculus
The surface area generated by a volume of revolution (for example, the surface of a sphere) can be approximated with calculus. One technique is to find a curve, that when rotated around an axis, creates the same shape as the surface area we are trying to find. We can then find the area of the surface of revolution with integration.
Surface Area of Revolution Formulas
If you have a non-negative smooth function on the closed interval [a, b], the surface area generated by revolving the curve around the x-axis between a and b is given by the following integral:
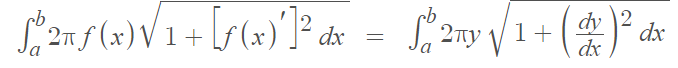
If you are revolving the curve around the y-axis, the integral becomes:
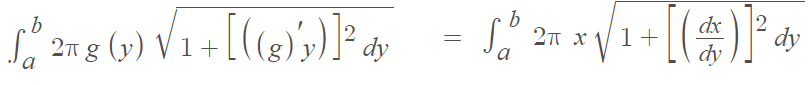
Example: What is the surface area created when y = x3 is revolved around the x-axis on [0, 2]?
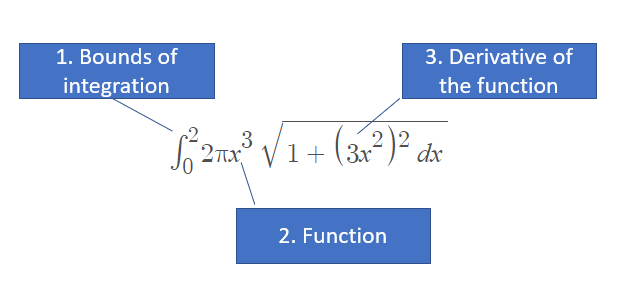
Step 1: Plug the given information into the formula. You have three parts to swap out: the bounds of integration, the given function, and the derivative of the function. For this example, the derivative of x3, which is 3x2 is found with the power rule:
Step 2: Integrate. This integral uses u-substitution and the product rule. The solution is 203 (Click here for a PDF of Solution Steps (Symbolab)).
Reasoning Behind the Formula for Surface Area
It may seem strange that you can integrate a three-dimensional shape, like a cone. Up until this point in calculus, you may have been integrating a simple area under a curve. However, nothing different is happening here. What you’re actually doing is flattening the cone, then integrating.
The underlying formula for finding the surface area begins with a right circular cone.
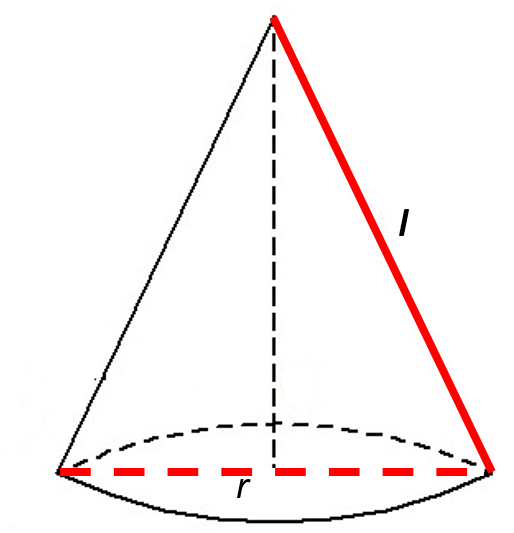
The formula for the flattened surface area (S) of this type of cone is [1]:
S = π r l.
To be able to integrate (find the area) with this formula, you slice the cone along the slant edge, (l in the above image) and flatten it.
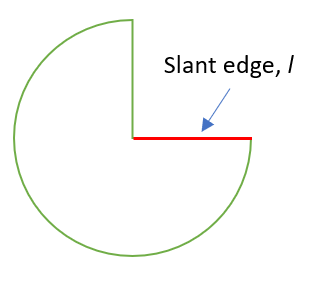
The key idea is that if we rotate a short, straight line segment, the basic shape is a right circular cone or a truncated cone (a cone with the top snipped off). Even if the slant edge of the cone if a curve, integrating gives a very good approximation for surface area.
References
3D Graph created with Desmos.com.
[1] Protter, M. & Protter, P. (1988). Calculus with Analytic Geometry. Jones & Bartlett.