Hypothesis Testing > False Discovery Rate
Contents:
- What is the False Discovery Rate?
- FDR Formula
- FDR in hypothesis testing
- FDR in medical testing
- Adjusting the false discovery rate
- Case Example
What is the False Discovery Rate?
The false discovery rate (FDR) is the expected proportion of type I errors. A type I error is where you incorrectly reject the null hypothesis; In other words, you get a false positive.
Closely related to the FDR is the family-wise error rate (FWER). The FWER is the probability of making at least one false conclusion (i.e. at least one Type I Error). In other words, it is the probability of making any Type I error at all. The Bonferroni correction controls the FWER, guarding against making one or more false positives. However, using this correction may be too strict for some fields and may lead to missed findings (Mailman School of Public Health, n.d.). The FDR approach is used as an alternative to the Bonferroni correction and controls for a low proportion of false positives, instead of guarding against making any false positive conclusion at all. The result is usually increased statistical power and fewer type I errors.
FDR Formula
The false discovery rate formula (Akey, n.d.) is:
FDR = E(V/R | R > 0) P(R > 0)
Where:
- V = Number of Type I errors (i.e. false positives)
- R = Number of rejected hypotheses
In a more basic form, the formula is just saying that the FDR is the number of false positives in all of the rejected hypotheses. The information after the | (“given”) symbol is just stating that:
- You have at least one rejected hypothesis,
- The probability of getting at least one rejected hypothesis is greater than zero.
False Discovery Rates in Hypothesis Testing
According to University of London’s David Colquhoun, “It is well know that high false discovery rates occur when many outcomes of a single intervention are tested.” Thanks to the power of computing, we can now test a hypothesis millions of times, which can result in hundreds of thousands of false positives.
For a more humorous (an perhaps understandable) look at the problems of repeated hypothesis testing and high false discovery rates, take a look at XKCD’s “Jelly Bean Problem.” The comic shows a scientist finding a link between acne and jelly beans, when a hypothesis was tested at a 5% significance level. Although there is no link between jelly beans and acne, a significant result was found (in this case, a jelly bean caused acne) by testing multiple times. Testing 20 colors of jelly beans, 5% of the time there is 1 jelly bean that is incorrectly fingered as being the acne culprit. The implications for false discovery in hypothesis testing is that if you repeat a test enough times, you’re going to find an effect…but that effect may not actually exist.
The odds of you getting a false positive result when running just 20 tests is a whopping 64.2%. This figure is obtained by first calculating the odds of having no false discoveries at a 5% significance level for 20 tests:
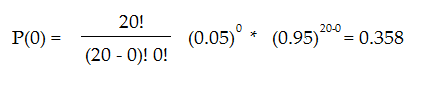
If the probability of having no false conclusions is 35.8%, then the probability of a false conclusion (i.e. a green jelly bean that causes acne) is 64.2%.
Back to top
False Discovery Rates in Medical Testing
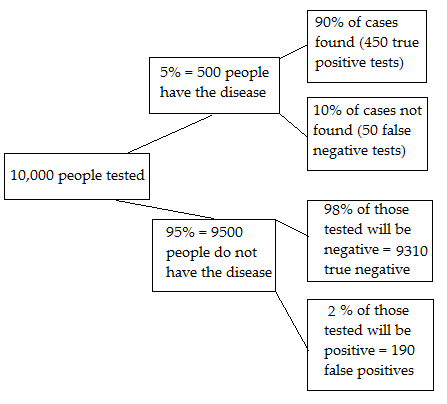
In medical testing, the false discovery rate is when you get a “positive” test result but you don’t actually have the disease. It’s the complement of the Positive Predictive Value(PPV), which tells you the probability of a positive test result being accurate. For example, if the PPV was 60% then the false discovery rate would be 40%. The image below shows a medical test that accurately identifies 90% of real diseases/cases. The false discovery rate is the ratio of the number of false positive results to the number of total positive test results. Out of 10,000 people given the test, there are 450 true positive results (box at top right) and 190 false positive results (box at bottom right) for a total of 640 positive results. Of these results, 190/640 are false positives so the false discovery rate is 30%.
Adjusting the false discovery rate
If you repeat a test enough times, you will always get a number of false positives. One of the goals of multiple testing is to control the FDR: the proportion of these erroneous results. For example, you might decide that an FDR rate of more than 5% is unacceptable. Note though, that although 5% sounds reasonable, if you’re doing a lot of tests (especially common in medical research), you’ll also get a large number of false positives; for 1000 tests, you could expect to get 50 false positives by chance alone. This is called the multiple testing problem, and the FDR approach is one way to control for the number of false positives.
The FDR approach adjusts the p-value for a series of tests. A p-value gives you the probability of a false positive on a single test; If you’re running a large number of tests from small samples (which are common in fields like genomics and protoemics), you should use q-values instead.
- A p-value of 5% means that 5% of all tests will result in false positives.
- A q-value of 5% means that 5% of significant results will be false positives.
The procedure to control the FDR, using q-values, is called the Benjamini-Hochberg procedure, named after Benjamini and Hochberg (1995), who first described it.
When not to correct
Although controlling for type I errors sound ideal (why not just set the threshold really low and be done with it?), Type I and Type II errors form an inverse of relationship; when one goes down, the other goes up and vice-versa. By decreasing the false positives, you increase the number of false negatives — that’s where there is a real effect, but you fail to detect it. In many cases, an increase in false negatives may not be an issue. But if false negatives are costly or vitally important for future research, you may not want to correct for false positives at all (McDonald, 2014). For example, let’s say you’re researching a new AIDS vaccine. A high number of false positives may be a hint that you’re on the right track, and it may indicate potential for future research on the vaccine. But if you overcorrect, you may miss out on those possibilities.
Back to top
Case Example: The False Discovery Rate
Mathematically, the probability of Type I Error is denoted by the lower-case Greek letter alpha, α. The percentage level for confidence is (1 – α) * 100%. So, an alpha-level of 0.05 is equivalent to a confidence level of 95%. The probability of Type II Error is denoted by the lower-case Greek letter beta, β. Power is 1 – β (not made into a percentage). So, for example, a beta level of 0.20 is equivalent to a power level of 0.80.
Imagine that there are 1000 hypotheses to be tested and that 100 of the Null Hypotheses are actually false and 900 of the Null Hypotheses are actually true. Let’s suppose that these are 1000 separate studies to determine whether certain foods and dietary supplements affect peoples’ health, and so each Null Hypothesis states that a certain food or dietary supplement has no effect on health. Assume an alpha-level of 0.05 is used (95% confidence). Also assume that the probability for Type II Error, beta, is 0.20 and so statistical power is 0.80. These are fairly realistic levels, although 0.80 power is probably higher (better) than many studies would have.
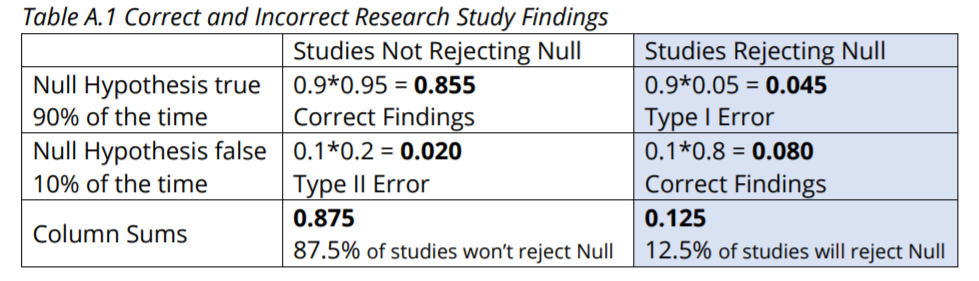
With a 0.05 alpha probability for Type I Error, expect 900 * 0.05 = 45 Type I Errors, and expect 900 * 0.95 = 855 correct non-rejections of the Null Hypothesis. With a 0.20 beta probability for Type II Error, expect 100 * 0.20 = 20 Type II Errors, and expect 100 * 0.80 = 80 correct rejections of the Null Hypothesis. Therefore, we expect a total of 45 + 80 = 125 rejected Null Hypotheses.
What percentage of the rejected Null Hypotheses do we expect to be erroneously rejected? This is our false discovery rate. Per the above, we expect 45 to be erroneously rejected, and we expect 80 to be correctly rejected. Therefore, we expect 45/(45 + 80) = 36% of the rejected Null Hypotheses to be erroneously rejected. Given that rejected Null Hypotheses tend to get all the publicity, you should find this eye-opening. (Headlines for rejected null hypotheses might be statements like “This supplement significantly improves health!” and “This food is a significant health risk!”)
We can also lay this out in a Table (A.1) of probabilities. Using the rightmost column to calculate the proportion of studies rejecting the Null Hypothesis that are Type I Errors gives us 0.045 / 0.125 = 0.360 = 36%.
The 36% can be improved upon by increasing the sample sizes in the 1000 studies. This will increase power. If we increase power to 0.9, for example, we’ll increase the correct rejections from 80 to 90. Ideally, if we can increase sample size sufficiently, we can set our alpha down to 0.01, thus decreasing the 45 to 9, while also maintaining or even increasing power. With alpha of 0.01, beta of 0.10 and thus power of 0.90, we would reduce the false discovery rate to 9 / (9 + 90) = 9%. This is much better, but it’s also much more expensive to gather the
large amounts of additional data that are required.
Lastly, keep in mind that the 36% false discovery rate we came up with is contingent on our assumption that only 100 of the 1000 Null Hypotheses are actually false. If researchers have good theories to guide their choice of hypotheses, then the proportion of Null Hypotheses that are truly false should be higher and the false discovery rate should be lower.
References
:
Akey, J. (n.d.). Lecture 10: Multiple Testing. Article posted on the University of Washington website. Retrieved October 29, 2017 from:http://www.gs.washington.edu/academics/courses/akey/56008/lecture/lecture10.pdf.
Benjamini, Y. & Hochberg, Y. (1995). Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society. Series B (Methodological) Vol. 57, No. 1, pp. 289-300
Colquhoun, D. An investigation of the false discovery rate and the misinterpretation of p-values. Published 19 November 2014. Available here.
Mailman school of Public Health (n.d.). Article posted on the Columbia University website. Retrieved 10/29/2017 from: https://www.mailman.columbia.edu/research/population-health-methods/false-discovery-rate
XKCD’s “Jelly Bean Problem.”
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. Retrieved October 29, 2017 from: http://www.biostathandbook.com/multiplecomparisons.html