Limit Does Not Exist: Why and How in Simple Steps

Contents:

• When Does a Limit Not Exist?
• How to find when the limit does not exist

When Does a Limit Not Exist?

In order for a limit to exist at a point c, it must settle on a certain value at that point. There are three main reasons for a limit not existing:

1. Wild oscillations: the function bounces between two x-values as x approaches c,
2. The function settles on two different numbers: one approaching from the left and a different one from the right as x approaches c.
3. unbounded behavior: the function increases or decreases without constraint as x approaches c.

1. Wild Oscillations

.

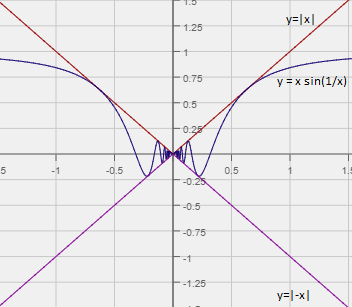
What’s important is that the values around a point settle towards a number, not that a particular function value exists. A case in point is y = x sin(1/x). Although the function value at x = 0 exists (it’s 0), the function varies wildly around that point. For example, testing a few values around 0, you get:

• y = .5 sin(1/.5) = 0.45
• y = 1 sin(1/1) = 0.84

Therefore, the limit doesn’t exist for y = x sin(1/x). However, you can make a good approximation with the Squeeze Theorem.

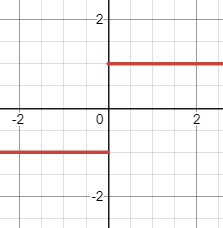
Function settles on two different numbers

The function settles on more than one number as you move in towards your chosen x-value from the left and right.

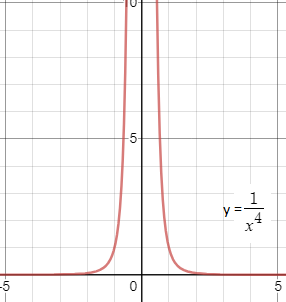
Unbounded behavior

Unbounded behavior of a limit refers to a function growing without bound (in other words, to infinity) at the limit point. The following image shows unbounded behavior near zero, where the y-values increase without bound:

How to Find When the Limit Does Not Exist

There are several ways to find out if a limit does not exist. From easiest to more challenging, they are:

1. Limit calculator
2. Graph the function
3. Create a table of values
4. Use algebra

1. Limit Calculator

This Wolfram widget will calculate the limit for you:

2. Graphing

Look at the graph. If the graph is going in completely different directions (i.e. up and down at the same point) at the particular x-value you are trying to find a limit for, the limit does not exist.

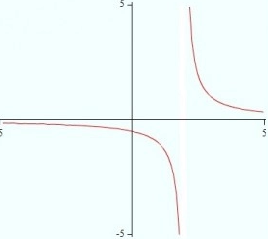
On a graphing calculator, zoom in on smaller and smaller increments to test the behavior of the graph (See: How to use zoom on the TI-89).

3. Using a Table

By hand, the easiest way to show a limit doesn’t exist is to calculate the one-sided limits; In other words, find the limit as it comes from the left, and find it as it comes from the right. For example, let’s say you have some function f(x) = [x] at x = 2, then find that:

• lim (x→2−) = 1
• lim (x→2+) = 2

Then the limit for f(x) does not exist.

Find the limit of the function on a TI-89 by building a table with small increments either side of the function’s value. For example, if you want to know if the limit exists at x = 1, then make your inputs several values around x = 1, like {0.9, 0.99, 1. 01, 1.1 }. If the table shows a trend to different numbers either side of the value, then the limit does not exist. See: How to Build a Table of Values on the TI-89.

4. Using Algebra to find when the limit does not exist

Use your algebra skills to look at the behavior of a function. For example, the limit of the function
y = (-1/(1-x)-cos(x))/(2cos(x)sin(x))
does not exist at x = 0. As the function approaches zero, the numerator approaches -2 and the denominator approaches 0. Using this logic, you can determine that the limit from the left is negative infinity and the limit from the right is infinity.

Tip: Technically, a limit doesn’t exist if the value at that function is infinity. But knowing that a number approaches infinity at a certain point is extremely useful, so we say that: lim f(x) = ∞.

Back to Top

Appendix

How to Use Zoom on the TI-89

1. Press ON.
2. Press the green button, then the F1 button at the top to access the ‘Y=’ command.
   
3. Type in your function.
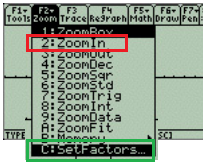
4. Press the F2 button for ZOOM options.
5. 
   
   Choose Zoom in. This recenters the graph, zooming in by the amount you specify in C: SetFactors. Use the arrows to scroll down to this setting. You may not need to change the settings; The default is 1/4 of the x-axis and y-axis (your scales will be 1/4 of what they were previously).

Limit Does Not Exist: References

Folk, D. (Undated). Graphing a Function on the TI-89. Retrieved May 25, 2019 from: https://emunix.emich.edu/~dfolk/Web_Page_Materials/Calculator_basics/TI89/Graphingbasicsti_89.html
Larson, R. & Edwards, B. (2009). Calculus. Cengage Learning.