A function that has a continuous derivative is differentiable; It’s derivative is a continuous function.
How do I know if I have a continuous derivative?
As the definition of a continuous derivative includes the fact that the derivative must be a continuous function, you’ll have to check for continuity before concluding that your derivative is continuous. If you don’t know how to do this, see:
How to check to see if your function is continuous.
Examples
Example of a function that has a continuous derivative:
The derivative of f(x) = x2 is f′(x) = 2x (using the power rule). This derivative has met both of the requirements for a continuous derivative:
- The initial function was differentiable (i.e. we found the derivative, 2x),
- The linear function f(x) = 2x is continuous.
Example of a function that does not have a continuous derivative:
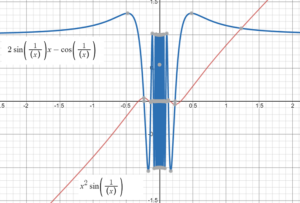
Not all continuous functions have continuous derivatives. The continuous function f(x) = x2sin(1/x) has a discontinuous derivative. So the derivative does not meet the definition of being a continuous derivative:
- The initial function is differentiable,
- The derivative is discontinuous.
Some functions behave even more strangely. The Blancmange function and Weierstrass function are two examples of continuous functions that are not differentiable anywhere (more technically called “nowhere differentiable“). Hermite (as cited in Kline, 1990) called these a “…lamentable evil of functions which do not have derivatives”.
Continuous and Differentiable
All differentiable functions (i.e., all functions with a derivative at every point in its domain) are continuous, but not all continuous functions are differentiable. The only way for the derivative to exist everywhere is if the function also exists on its domain.
Just because a function is continuous doesn’t mean its derivative is defined everywhere. On the other hand, if a derivative exists everywhere, that must mean that the function exists everywhere, thus “continuous and differentiable.”
References
Kline, M. Mathematical Thought from Ancient to Modern Times. Oxford, England: Oxford University Press, 1990.
Chapter 4. Differentiable Functions. Retrieved November 2, 2019 from: https://www.math.ucdavis.edu/~hunter/m125a/intro_analysis_ch4.pdf
Norden, J. Continuous Differentiability. Retrieved November 2, 2015 from: https://www.desmos.com/calculator/jglwllecwh
Desmos Graphing Calculator (images).
Oldham, K. et al. (2008). An Atlas of Functions. Springer.