The Edgeworth series distribution is a continuous probability distribution that approximates a probability distribution in terms of its cumulants and Hermite polynomials [1]. It relates the probability density function (PDF) to a standard normal distribution PDF. It is sometimes seen in statistical asymptotic theory, where approximations to sample statistic distributions of order greater than n-1/2 are calculated [2].
The PDF for the bivariate Edgeworth series distribution (BVESD) is [3]
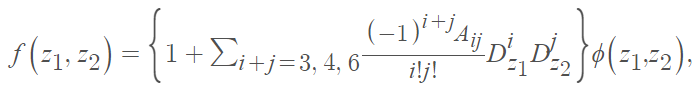
Where
- φ(z1, z2) is the standard bivariate normal density function,
- Aij’s are functions of the population cumulants, and
- Dz1, Dz2 are partial derivative operators.
The characteristic function is:
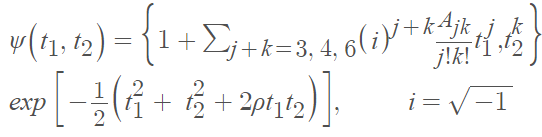
It is a challenge to generate samples from the PDF of the Edgeworth series distribution. In addition, the distribution of the conditional probability of misclassification for the ESD is intractable because of the expression’s complex nature. Related to the Edgeworth form of distribution are the Cornish-Fisher expansions, although it has no general theoretical superiority [3].
The ESD has been used for some practical purposes, including the study of nonlinear gust loading factors (used in the design of structures exposed to extreme winds) [4].
Edgeworth Series
Edgeworth distributions are derived from an Edgeworth series, a type of series that can be used to approximate a probability distribution [5]. They are typically used to approximate distributions that are not normally distributed, such as the binomial distribution or the Poisson distribution.
References
[1] Skhakti, P. A Lexicon of probability distributions.
[2] A. Adeyeye. Asymptotic Distribution of Probabilities of Misclassification for Edgeworth Series Distribution (ESD). Engineering Mathematics. 2020; 4(1): 1-9 http://www.sciencepublishinggroup.com/j/engmath doi: 10.11648/j.engmath.20200401.11
[3] S. Kocherlakota , K. Kocherlakota & N. Balakrishnan (1985) Effects of nonnormality on the spart for the correlation coefficient: bivariate edgeworth series distribution, Journal of Statistical Computation and Simulation, 23:1-2, 41-51, DOI: 10.1080/00949658508810857
[4] Johnson, Kotz, and Balakrishnan, (1994), Continuous Univariate Distributions, Volumes I and II, 2nd. Ed., John Wiley and Sons.
[5] Wolfram. Edgeworth Series.