Matrix Function: Simple Definition, Examples

Types of Functions >

There are many ways to define a matrix function (or matrix-valued function). One way is that the function has the form of a matrix, but instead of numbers inside the matrix there are functions. For example, A(t) is a 2 x 2 matrix function:


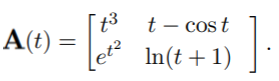
The function is defined only for t values that define all 4 of the elements in this example matrix.

Another way to define a matrix function is simply as a function that calculates a (usually square) matrix A; To put that another way, it’s a function that maps one matrix to another. Some authors define matrix functions on the complex plane ℂ. For example Higham (2008) highlights the definition that it involves a scalar function f and a matrix A ∈ ℂ^{n x n}; the combination calculates a matrix the same dimensions as A.

An entire matrix function calculates a matrix and the action of that matrix on a vector (Schilders, et al., 2008). Matrix functions play an important role in control theory and the theory of differential equations.

Matrix Function Examples

• The powers A^p, where A is an n x n matrix, are all matrix functions (Abadir & Magnus, 2005).
• The identity function f(t) = t is a monotone matrix function for every real interval (Johnson, 1990).

Matrix Functions by Infinite Series

A matrix function for square matrices A can be defined by the infinite series


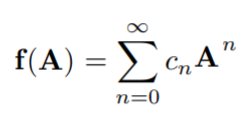
as long as there is a finite limit (Peterson & Pedersen, 2005).

References

Abadir, K. & Magnus, J. (2005). Matrix Algebra. Cambridge University Press.
Higham, N. (2008). Functions of Matrices: Theory and Computation (Other Titles in Applied Mathematics). Society for Industrial and Applied Mathematics.
Johnson, C. (1990). Matrix Theory and Applications. Proc Held Phoenix, Jan 10-11, 1989 (Proceedings of Symposia in Applied Mathematics). American Mathematical Society.
Peterson, K. & Pedersen, M. (2005). The Matrix Cookbook. Retrieved January 21, 2021 from: https://www.ics.uci.edu/~welling/teaching/KernelsICS273B/MatrixCookBook.pdf
Schilders, W. et al., (2008). Model Order Reduction: Theory, Research Aspects and Applications. Springer Berlin Heidelberg.