Contents:
What is a Moment?
Watch the video for an overview of moments:
The most common definitions you’ll come across for moments include:
- The first is the mean(average),
- The second is a measure of how wide a distribution is (the variance).
For most basic purposes in calculus and physics, these loose definitions are all you’ll need. However, it’s important to know that there are two different kinds of “moment”: raw moments (moments about zero) and central moments. They are defined differently.
- The rth moment about the origin of a random variable X = μ′r = E(Xr). The mean (μ) is the first moment about the origin.
- The rth moment about the mean of a random variable X is μr = E [(X – μ)r ]. The second moment about the mean of a random variable is the variance (σ2).
Formula.
The rth moment = (x1r + x2r + x3r + … + xnr)/n.
This type of calculation is called a geometric series. You should have covered geometric series in your college algebra class. If you didn’t (or don’t remember how to work one), don’t fret too much; In most cases, you won’t have to actually perform the calculations. You just have to have a general grasp of the meaning. The formula might look a little daunting, but all you have to do is replace the exponent “r” with the number of the moment you’re trying to find. For example, if you want to find the first moment, replace r with 1. For the second moment, replace r with 2.
First Moment (r = 1).
The 1st moment around zero for discrete distributions = (x11 + x21 + x31 + … + xn1)/n
= (x1 + x2 + x3 + … + xn)/n.
This formula is identical to the formula to find the sample mean in statistics. You add up all of the values and divide by the number of items in your data set.
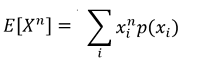
For continuous distributions, the formula is similar but involves an integral:
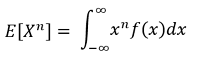
Second Moment (r = 2)
The 2nd moment around the mean = Σ(xi – μx)2.
This is equal to the variance.
The Σ symbol means to “add up”. See: What is sigma notation?
In practice, only the first two moments are ever used in statistics. Several more moments are common in physics:
Third (s = 3).
The 3rd moment (skewness) = (x13 + x23 + x33 +… + xn3)/n
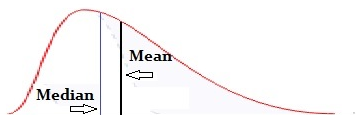
Skewness gives you information about a distribution’s “shift”, or lack of symmetry. Distributions with a left skew have long left tails; Distributions with a right skew have long right tails.
4th
The fourth is kurtosis. Kurtosis tells you how a data distribution compares in shape to a normal (Gaussian) distribution (which has a kurtosis of 3).
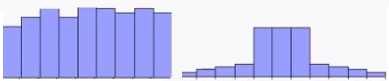
- Positive kurtosis = a lot of data in the tails.
- Negative kurtosis = not much data in your tails.
Higher R.
Higher-order terms (above the 4th) are difficult to estimate and equally difficult to describe in layman’s terms.
For example, the 5th r measures the relative importance of tails versus center (mode, shoulders) in the cause of a distribution’s skew.
- A high 5th = heavy tail, little mode movement
- Low 5th = more change in the shoulders.
In calculus based statistics, the first two moments of distribution are most important. The mean tells us what the average values look like, and the variance tells us about the spread.
In physics, all moments are used, including higher-order n. Sometimes they are calculated from the definition; other times they are calculated using an MGF.
Rth Moment of a Distribution: Notation
- When r = 1, we are looking at the first moment of a distribution X. We’d write this simply as μ, and we can write μ = E(X). This is just the mean of the distribution.
- For r = 2, we have the second moment. This happens to be the variance of our distribution. We can write this as μ2‘= EX2, but usually we just write it as σ2.
Moment Generating Function (MGF) & Probability Generating Function (PGF)
Contents (Click to skip to that section):
1. What is a Moment Generating Function?
Moment generating functions (MGFs) are a way to find moments like the mean(μ) and the variance(σ2). They are an alternative way to represent a probability distribution with a simple one-variable function.
Each probability distribution has a unique MGF, which means they are especially useful for solving problems like finding the distribution for sums of random variables. They can also be used as a proof of the Central Limit Theorem.
There isn’t an intuitive definition for exactly what an MGF is; it’s just a computational tool. Think of it as a formula, in the same way that y = mx + b allows you to create linear functions, the MGF formula helps you to find moments.
How to Find an MGF
Finding an MGF for a discrete random variable involves summation; for continuous random variables, calculus is used. It’s actually very simple to create moment generating functions if you are comfortable with summation and/or differentiation and integration:
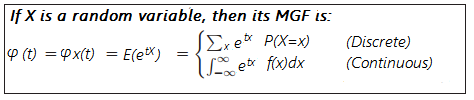
For the above formulas, f(x) is the probability density function of X and the integration range (listed as -∞ to ∞) will change depending on what range your function is defined for.
Example: Find the MGF for e-x.
Solution:
Step 1: Plug e-x in for fx(x) to get:
![]()
Note that I changed the lower integral bound to zero, because this function is only valid for values higher than zero.
Step 2: Integrate. The MGF is 1 / (1-t).
The moment generating function only works when the integral converges on a particular number. The above integral diverges (spreads out) for t values of 1 or more, so the MGF only exists for values of t less than 1. You’ll find that most continuous distributions aren’t defined for larger values (say, above 1). This is usually not an issue: in order to find expected values and variances, the MGF only needs to be found for small t values close to zero.
Using the MGF
Once you’ve found the moment generating function, you can use it to find expected value, variance, and other moments.
- M(0) = 1,
- M′(0) = E(X),
- M′′(0) = E(X2),
- M′′′(0) = E(X3)
and so on;
Var(X) = M′′(0) − M′(0)2.
Example: Find E(X3) using the MGF (1-2t)-10.
Step 1: Find the third derivative of the function (the list above defines M′′′(0) as being equal to E(X3); before you can evaluate the derivative at 0, you first need to find it):
M′′′(t) = (−2)3(−10)(−11)(−12)(1 − 2t)-13
Step 2: Evaluate the derivative at 0:
M′′′(0) = (−2)3(−10)(−11)(−12)(1 − 2t)-13
= (−2)3(−10)(−11)(−12)(1)
= 10,560.
Solution: E(X3) = 10,560.
What is a Probability Generating Function?
A probability generating function contains the same information as a moment generating function, with one important difference: the probability generating function is normally used for non-negative integer valued random variables.
References
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 145-149, 1984.