Average Value of a Function (Using an Integral)

Problem Solving > Average Value of a Function

1. Definition of Average
• TI 89 Graphing Calculator Steps
2. Average of a Function

1. Average Definition

The average is one measure of the center of a set of data.

A simple formula, which works for most situations, is:

average = total sum of all the numbers / number of items in the set.

More formally, the formula is written as:


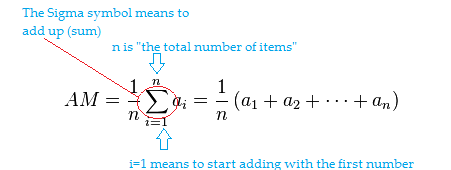
The summation sign (Σ) means to “add up”. Here, the letter n is used to represent the number of items. You can use this formula to get to the exact same answer as in the problem above:
Average = ⅓ * (2 + 4 + 6) = 12.

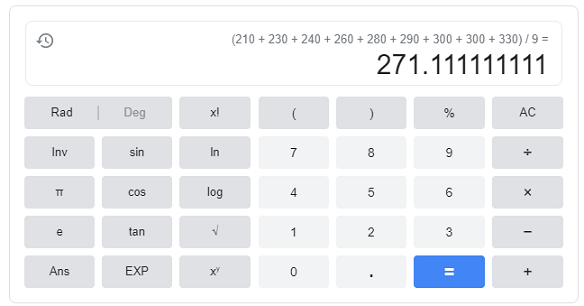
Example: Find the average: 210, 230, 240, 260, 280, 290, 300, 310, 330.
Solution:

1. Sum up the numbers: 210 + 230 + 240 + 260 + 280 + 290 + 300 + 300 + 330 = 2450
2. Divide Step 1 by the number of items in your set (9): 2450 / 9 = 271.11

The arithmetic mean has the distinct disadvantage of being extremely influenced by outliers —very small, or very large data points. For example, let’s say you have: 11, 12, 22, 40, 70 and 15,000.
The mean is: (11 + 12 + 22 + 40 + 70 + 15,000) / 6 = 2526, a poor reflection of the center point.

The median is resistant to outliers; the middle of this set is 26: in between the 22 and 40. Whether you use the mean or the median depends on lots of factors (including your instructor’s preferences), but in general, don’t use the average if you have outliers.

Find the Mean on the TI 89 Graphing Calculator

Example problem: Find the mean: 12, 23, 78, 98, 121, 342, 88, 7, 27.

Step 1: Press the HOME button.

Step 2: Press CATALOG.

Step 3: Press ALPHA , then 5. This should bring you to the letter M in the catalog.

Step 4: Scroll to “mean(” and press ENTER.

Step 5: Press 2nd then (.

Step 6: Enter your data. Each number should be separated by a comma.

Step 7: Press the 2nd key, then ).

Step 8: Press ENTER to get 796/9.

Note: For a decimal solution, press the diamond key, then press ENTER. The decimal solution is 88.4444.

Lost your guidebook? You can download a new one from the TI website here.

How to Find Average Value of a Function (with Integrals)

When it comes to finding the average value of a function, the simple formula given above doesn’t work. That’s mainly because the formula works for discrete variables, and a function is usually continuous. However, finding the average value of a function is relatively simple, if you’re comfortable with integration. Note that in order for the formula to work, you must have an integrable function that is also a continuous function.

Let’s say you wanted to find the average height of a graph of a function (f) over an interval from a to b.  The formula is:

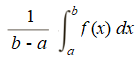
The integral is really just the area under a curve. The idea is that you’re taking infinitely many slices of this area under a curve and finding a tiny sliver that represents the average.

Average Value of a Function: Example

Example question: Find the average value of a function f(x) = 3x² – 2x on the closed interval [2, 3].

Step 1: Insert the given function into the formula:

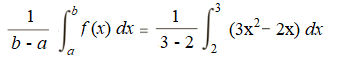
• The function itself (3x² – 2x) replaces the f(x) on the right side of the equation.
• The given upper limit (4) and lower limit (1) replace the b and a in two places: the denominator on the left side of the equation and the upper and lower integral on the right side.

Step 2: Solve the integral using the usual rules for integration. Solve this particular integral using the power rule for integrals.

For 3x², the constant moves to the front of the integral symbol and integrates to zero, leaving ∫x² = x³ / 3.

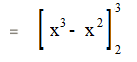
Step 3: Evaluate the function at the given limits of integration (3 and 2).

(27 – 9) – (8 – 4) = 18 – 4 14.

This step is easier than it looks:

1. Plug the upper limit of integration (3) into the formula you obtained in Step 2.
2. Repeat for the lower limit of integration (2).
3. Subtract the two terms as shown.

References

Larson, R. (2011). Calculus 1 with Precalculus. Cengage Learning; 3 edition.